跳转到:
控制变量概览
控制变量是模型中不属于处理变量的变量。控制变量用于估计基准结果,即在每个处理变量针对所有地理位置和时间段都设置为基准值的反事实情景下,会发生的预期结果。(对于媒体变量,基准值始终为零,但对于非媒体处理变量,基准值通常不为零。)使用控制变量可以更准确地估计基准结果,以及处理变量对该结果的因果效应。
控制变量可分为以下几类:
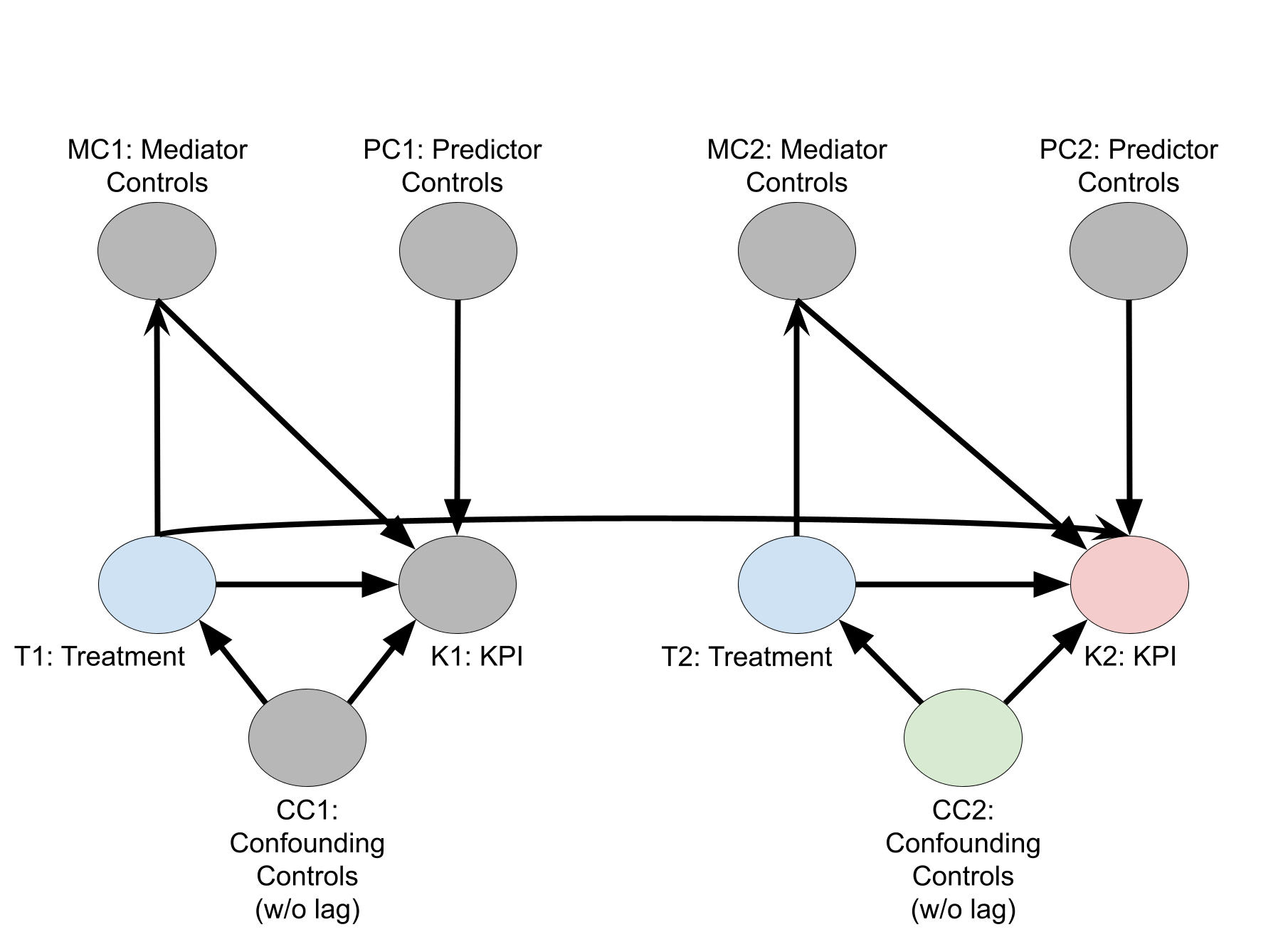
混杂变量:对处理变量和 KPI 都有因果效应。纳入这些变量可以消除处理变量对 KPI 的因果估计偏差。
预测变量:对 KPI 有因果效应,但没有其他效应。纳入这些变量对于消除处理变量的因果效应偏差毫无作用。不过,强预测变量可以减少因果估计值的方差。
另一种变量类型是中介变量。这类变量是位于处理变量与 KPI 之间的因果路径中的变量。也就是说,它们对 KPI 有因果效应,并且受处理变量的因果影响。不应将中介变量纳入为控制变量,因为纳入中介变量会导致对处理变量的因果推理估计出现偏差。
下面的因果有向无环图 (DAG) 说明了不同变量类型之间的因果关系,目的是让您了解媒体对 KPI 的因果效应。在节点名称中,数字 1 表示时间段 1 的变量值,数字 2 表示时间段 2 的变量值,依此类推。该图仅显示了时间段 1 和 2 的节点,但我们可以假设它持续了 \(T\) 个时间段。
选择控制变量
营销组合建模分析 (MMM) 的目的是针对媒体效应(而不是预测准确率)进行因果推理。因此,控制变量的主要目的是更好地推断处理变量对 KPI 产生的因果效应。您无需纳入所有可能会提高样本内或样本外预测准确率的预测变量,也不建议您这样做。预测准确率的小幅提高并不能保证因果推理准确率的提高。过多的预测变量可能会使因果估计值的方差虚增,并可能会增加因模型误设而造成偏差的风险。
在通过集思广益来确定可能需要将哪些混杂变量纳入模型中时,建议的做法是专注于确定会影响营销决策或决策者会考虑的变量。原因是,会影响营销决策的大多数变量也会对 KPI 产生效应,因此属于混杂变量。相反,几乎不可能完整列出会影响 KPI 的变量,而且除非这些变量也会影响营销决策,否则它们不是混杂变量。
原则上,营销经理可以提供一份用于制定预算决策的所有可量化信息的清单,但在现实中可能很难编制出一份完整的清单。您可以向营销经理提出以下基本问题:
- 在年度或季度层面,他们是如何决定媒体总预算的?
- 他们如何决定各媒体渠道的分配比例?
- 在每一年中,他们如何确定预算较高和较低的周?
- 是否存在与节假日或产品发布等特定事件相对应的支出高峰?
- 对于问题 1-4,哪些数据源与预算决策最相关?例如,往年的 KPI 值或经济变量?
- 是否存在任何自然媒体,以及是什么影响了投放自然媒体的决策?
- 是否存在任何非媒体处理变量(例如价格变动或促销活动),以及他们如何决定何时以及如何应用这些变动?
最终,关于控制变量,我们对您有如下建议:
- 纳入混杂变量。
- 排除中介变量。
- 纳入可减少因果估计值方差的强预测变量。
- 不要仅仅为了优化预测准确率而纳入过多的变量,因为这会增加因模型误设而造成偏差的风险。
提取控制系数的后验和先验样本
控制系数的先验和后验样本存储在 Meridian 对象中,提取后可以创建区间或其他摘要指标,帮助您确定哪些控制变量是相关的。
如果 Meridian 对象的名称为 mmm,则可以分别借助 mmm.inference_data.prior.gamma_c 和 mmm.inference_data.posterior.gamma_c 来查找控制系数的先验样本和后验样本。
纳入搜索查询量作为控制变量
如选择控制变量中所述,若要消除处理变量对 KPI 产生的因果效应的偏差,有必要纳入混杂变量。此外,若要获得无偏差的因果估计值,也有必要排除中介变量。对于某些媒体渠道,搜索查询量可能是中介变量;但对于其他媒体渠道,则可能是混杂变量。例如,搜索查询量肯定是搜索广告的混杂变量,因为相关搜索查询往往是展示搜索广告的先决条件。但是,其他形式的媒体也能促成搜索行为,因此搜索查询量对于这些媒体渠道来说是中介变量。如需了解详情,请参阅付费搜索建模。
由于您希望估计所有处理变量的综合效应,因此您需要使用单个模型进行推理。您必须在下列做法中二选一:假设搜索查询量是混杂变量,并将其纳入模型;假设搜索查询量是中介变量,并将其排除在模型之外。您所选择的假设应基于以下考虑因素:
- 对于获得无偏差估计值而言较为重要的渠道
- 处理变量、搜索查询量和 KPI 之间关系的假设强度
- 假设在多少渠道中搜索查询量是混杂变量而非中介变量
我们认为,由于搜索查询量与搜索媒体之间关系的相对强度,假设搜索查询量是混杂变量并将其纳入模型中,往往是正确的决策。不过,这一决策取决于应用场景。
使用滞后变量
对于某些控制变量 \(Z\)来说,纳入滞后值是有意义的。例如,在每一周 \(t\)中,针对某些 \(L\)值纳入 \(Z_{t-1},\dots ,Z_{t-L}\)。我们建议,只有当您认为滞后值 \(t-1, \dots ,t-L\) 对第 \(t\)周的 KPI 有因果效应时才这样做。
不需要滞后控制变量的情况
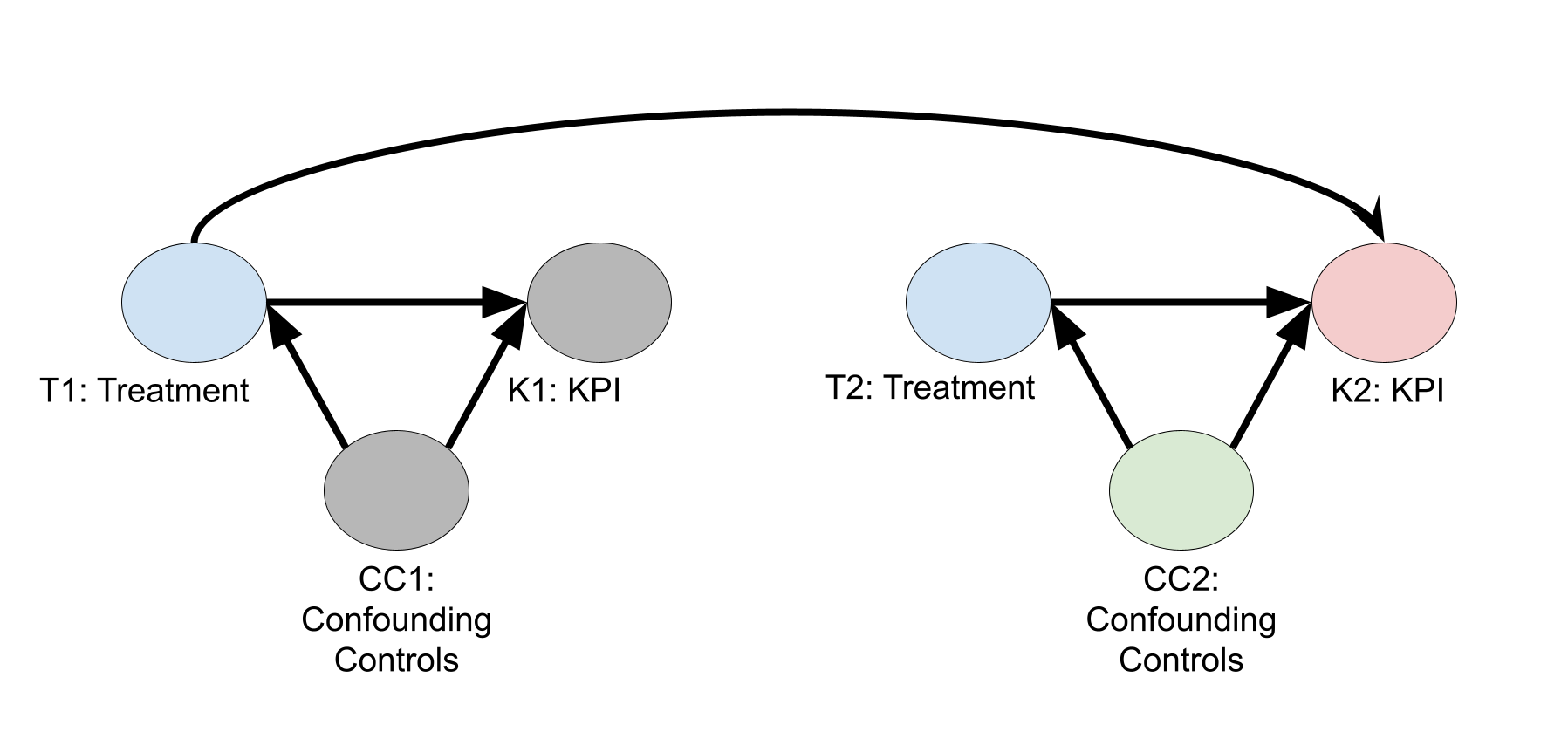
下图显示了一个因果有向无环图 (DAG),其中假设处理变量具有滞后效应,但控制变量并不具有滞后效应。假设此 DAG 无需滞后控制变量。在节点名称中,数字 1 表示时间段 1 的变量值,数字 2 表示时间段 2 的变量值。该图仅显示了时间段 1 和 2 的节点,但我们可以假设它持续了 \(N\) 个时间段。
利用“后门标准”(Pearl, J.,2009 年),您可以通过拟合回归模型来估计\(E\bigl( K2 \big| T2,T1,C2 \bigr) = E\bigl( K2^{(T2, T1)} \big| C2 \bigr)\),从而估计处理变量对第 2 周 KPI 产生的因果效应。不需要之前的控制变量 (\(C1\))。
需要滞后控制变量的情况
下图是需要滞后控制变量的因果 DAG。同样,节点名称中的数字对应于时间段。若要估计处理变量对第 2 周 KPI 产生的因果效应,您必须以对 KPI 有滞后效应的第 1 周控制变量为条件。如果不这样做,就会留下一条畅通无阻的路径 \(T1 \leftarrow L1 \rightarrow K2\)。利用后门标准,您可以通过拟合回归模型来估计 \(E\bigl( K2 \big| T2,T1,C2,L2,L1 \bigr) = E\bigl( K2^{(T2,T1)} \big| C2,L2,L1 \bigr)\)。
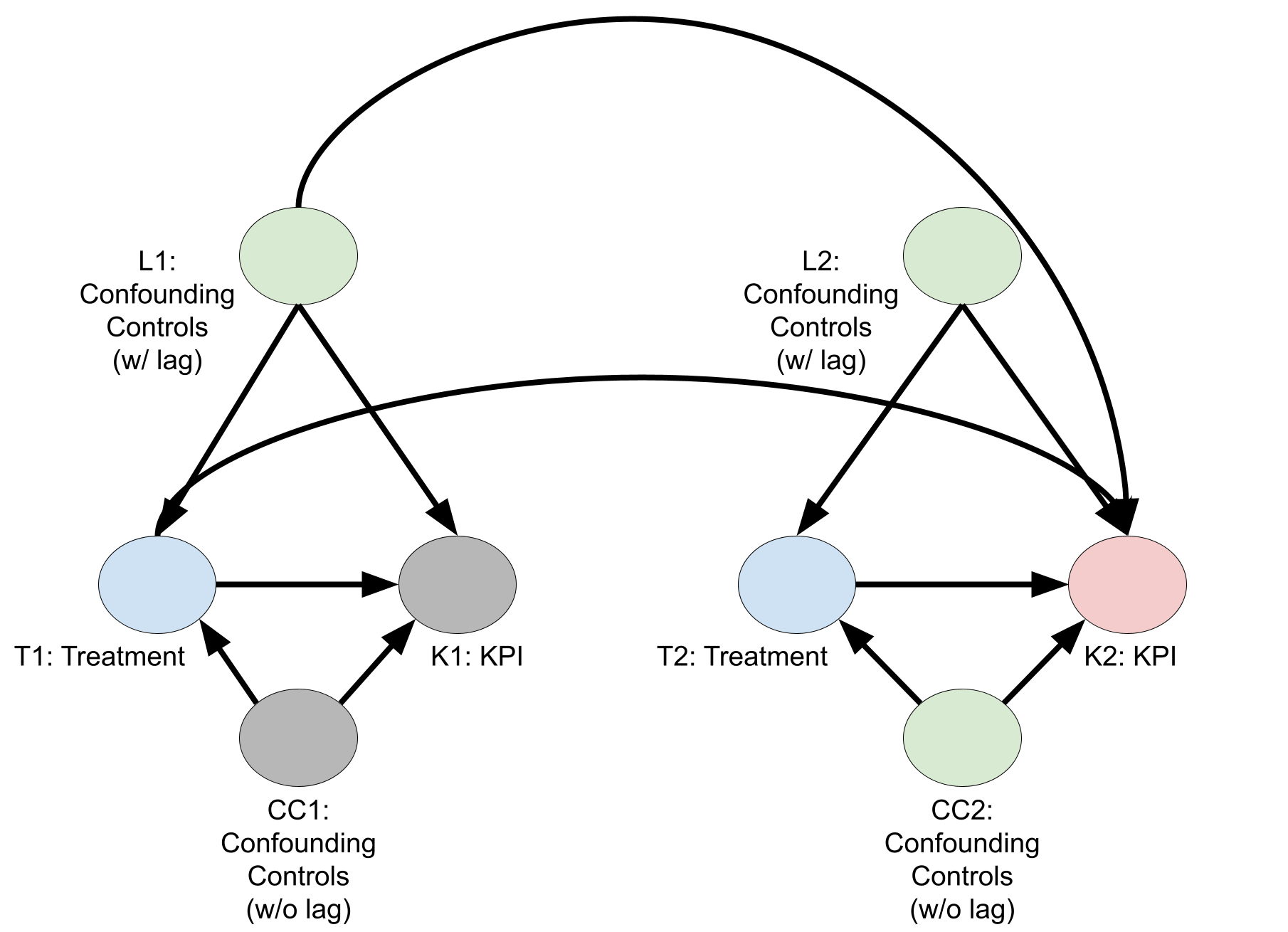
上图是一个简化后的双周 DAG,但一般来说,对于每一周\(t\),您都应当纳入第 \(t,t-1, \dots ,t-L\)周的控制变量,其中\(L\) 是控制变量仍被认为会影响 KPI 的最长滞后期。 \(L\) 的值可能因控制变量而异。
在实践中,可以在合理的值处截断 \(L\) ,以防止因添加过多变量而导致模型方差虚增。在很多情况下,如果滞后效应相对较弱,完全忽略滞后控制变量也是合理的。这种模型简化可以看作是偏差与方差之间的权衡。
按人口比例调整控制变量
默认情况下,KPI 以及付费和自然媒体执行会按人口比例调整。控制变量默认不会按人口比例调整,因为某些控制变量(例如温度)不应当按人口比例调整。不过,某些控制变量(例如竞争对手的展示次数)应当按人口比例调整,以便最大限度提高与按人口比例调整的 KPI 以及媒体变量的相关性。可以使用 ModelSpec 中的 control_population_scaling_id 实参按比例调整此类变量。同样,非媒体处理变量默认不会按比例调整。可以使用 ModelSpec 中的 non_media_population_scaling_id 按比例调整此类变量。
控制变量没有因果推理或基准细分的原因
Meridian 中提供付费媒体、自然媒体和非媒体处理变量的因果效应和贡献百分比。根据因果图,这些变量类型的回归效应可以解释为因果效应。不过,控制变量的回归效应不能解释为因果效应。因此,Meridian 不会估计控制变量的因果效应或贡献百分比。
此外,Meridian 不会按控制变量将基准结果分解为分配百分比。当然,某些控制变量对模型预测准确率的影响要大于其他变量。不过,这更多地与每个变量在预期结果估计值中贡献的方差相关,而不是与预期结果计算中每个变量的加性分量相关。实际上,对于控制变量,如何定义基准结果分配并不明确。一种可能的定义是,在每个地理位置和时间段,将每个控制变量设置为零时,预期结果发生的变化。不过,此数量没有实际意义,因为它既不表示控制变量的因果效应,也不表示其预测重要性。此外,对于每个控制变量,零值可能没有实际意义(甚至不可能出现),这进一步模糊了解释。
在预期结果计算中,一个变量可能具有较大的系数和加性分量,但作为 KPI 的预测因素,重要性却极低。对于方差较小的变量,情况尤其如此。如果变量的加性效应可以吸收到截距中,那么从模型中移除此类变量对预期结果估计值的影响可能微乎其微。
如需详细了解这些变量类型,请参阅自然媒体和非媒体处理变量。
