必要假设部分中指出,如果假设因果图满足后门标准,则条件可交换性假设成立。
因果图显示了变量之间的关系。变量会被划分到集合(节点)中,节点之间的箭头表示箭头方向可能存在因果效应。箭头不一定表示每对变量之间存在因果关系,但确实表示任何一对变量之间都不可能存在反向因果关系。
后门标准(Pearl, J.,2009 年)指出,给定一个因果图,如果一组变量 \(Z\) 同时符合以下条件,则相对于处理变量 \(X\) 和响应变量 \(Y\) ,此组变量满足后门标准:
- \(Z\) 中的任何节点都不是 \(X\)的后代,且
- \(Z\) 会阻断 \(X\) 和 \(Y\) 之间包含指向 \(X\)的箭头的每条路径
营销组合建模分析 (MMM) 用于估算付费媒体、自然媒体和非媒体变量对某个 KPI(例如销售额)的因果效应。因此付费媒体、自然媒体和非媒体变量是处理变量 (\(X\)),而 KPI 是响应变量 (\(Y\))。为了通过 MMM 回归估算这种因果效应,MMM 必须以一组精心选择的满足后门标准的控制变量为条件。以下是对后门标准条件的简述:
- 不得控制任何中介变量。中介变量是位于 \(X\) 和 \(Y\)之间的因果路径中的变量。
- 必须控制所有混杂变量。混杂变量是指对 \(X\) 和 \(Y\)都有因果效应的变量。
MMM 处理变量是付费媒体、自然媒体和非媒体处理变量的任意组合的集合,这些变量会基于地理位置和时间进行指数化处理。在一个图表中表示整个处理变量不太方便,因此可以考虑使用一个简化的图表,仅显示单个地理位置内的两个时间段。假设地理位置是独立的,因此同一图表可用于表示任何地理位置,且地理位置之间没有任何箭头或关系。两个时间段足以描述滞后处理效应的模式,您可以假设这种模式会在未来无限重复(或达到滞后时长上限)。
在下图中, \(T\) 表示付费媒体、自然媒体和非媒体处理变量, \(C\) 表示控制变量, \(K\) 表示 KPI。每个变量后面的数字表示时间段。在每个时间段内,假设处理变量会影响销售额,而控制变量会影响处理变量和销售额。在下图中,之前时间段的 \(T\) 会影响当前时间段的销售额(“滞后效应”)。Meridian 回归模型会将 Adstock 应用于付费媒体和自然媒体,但不会应用于非媒体处理变量。这实际上是假定非媒体处理变量不会产生滞后效应。在节点 \(T\) 中包含非媒体处理变量仍然有效,因为箭头表示连接节点中的任意一对变量之间可能存在因果效应。在节点 \(T\) 中添加非媒体处理变量会使 DAG 更清晰地呈现相关信息,并且 DAG 仍然可用于确定哪些变量满足后门标准。
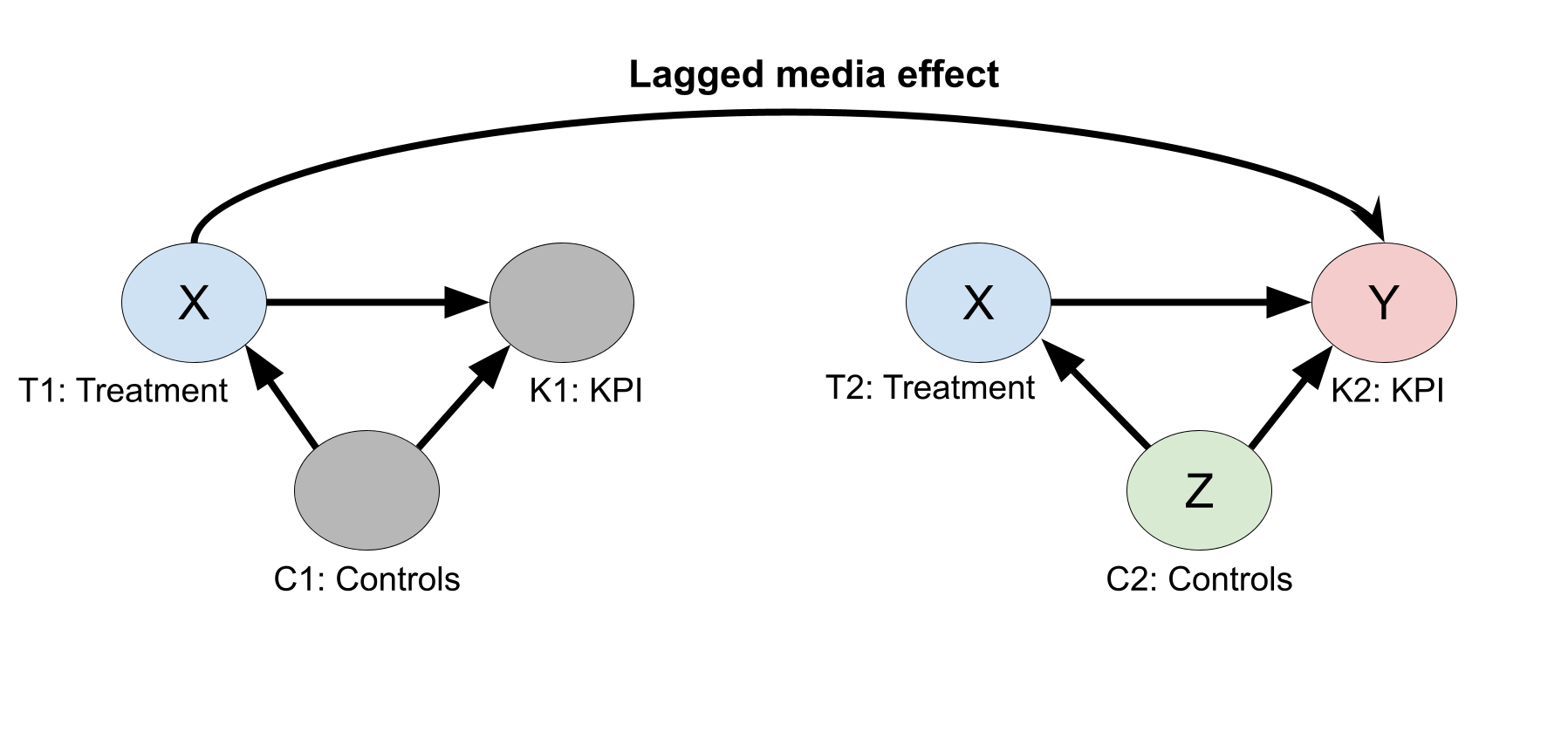
假设您要估算处理变量(\(T1\) 和\(T2\))对时间段 2 (\(K2\)) 的 KPI 的因果效应。从图表中可以看出,时间段 2 的控制变量 (\(C2\)) 满足后门标准。
可得出以下主要结论:对于每个时间段,MMM 回归应基于以下条件:
- 来自当前时间段和所有之前时间段的付费和自然媒体(时间段范围不超过滞后时长上限)。
- 仅当前时间段的非媒体处理变量。
- 仅当前时间段的控制变量。
需要注意以下细节:
- 从 \(C1\) 到 \(C2\) 的箭头不表示回归中要包含哪些变量。
- 从 \(C1\) 到 \(K2\) 的箭头要求回归包含滞后控制变量。在实践中,如果可能的话,最好避免这种情况,因为这可能会显著增加回归形参的数量。
- 从 \(T1\) 到 \(C2\) 的箭头有问题。在本例中, \(C2\) 既是中介变量,也是混杂变量。单个 MMM 回归模型无法用于恢复因果合并处理效应。
- 添加路径 \(T2 \leftarrow K1 \rightarrow K2\) 也是有问题的,原因相同。在本例中, \(K1\) 既是中介变量,也是混杂变量。
