本部分将介绍 Meridian 的关键指标 - 增量效果、投资回报率 (ROI)、边际投资回报率 (mROI) 和响应曲线。
内容要点
增量效果、投资回报率 (ROI)、边际投资回报率 (mROI) 和响应曲线都有助于您根据模型的发现结果制定出切实可行的业务策略。它们可为您解答最关键的营销问题:“我的渠道效果如何?”以及“接下来我应将预算投到何处?”
了解这些指标后,您可以确定效果最佳的渠道、了解当前的饱和度,并优化预算以最大限度地提升业务成效。特别是响应曲线,它以非常直观的方式展示了增量效果如何随支出的增加而变化,这是基于数据分配预算的基础。
营销示例
假设您经营一家鞋品网店。您在某个视频媒体渠道上花费了 10,000 美元。运行 Meridian 模型后,您发现该渠道带来了 25,000 美元的增量销售额。
- 增量效果是指营销活动带来的价值。例如,您的总销售额为 15 万美元,但 Meridian 估计,假如没有投放该广告系列,销售额则应为 12.5 万美元。这两者的差值就是增量效果,即 2.5 万美元。
- 您的投资回报率为 2.50(25,000 美元销售额/10,000 美元费用),这意味着您每花费 1 美元可赚取 2.50 美元。(如需详细了解此指标的计算方式,请参阅解读投资回报率和响应曲线时的注意事项)。
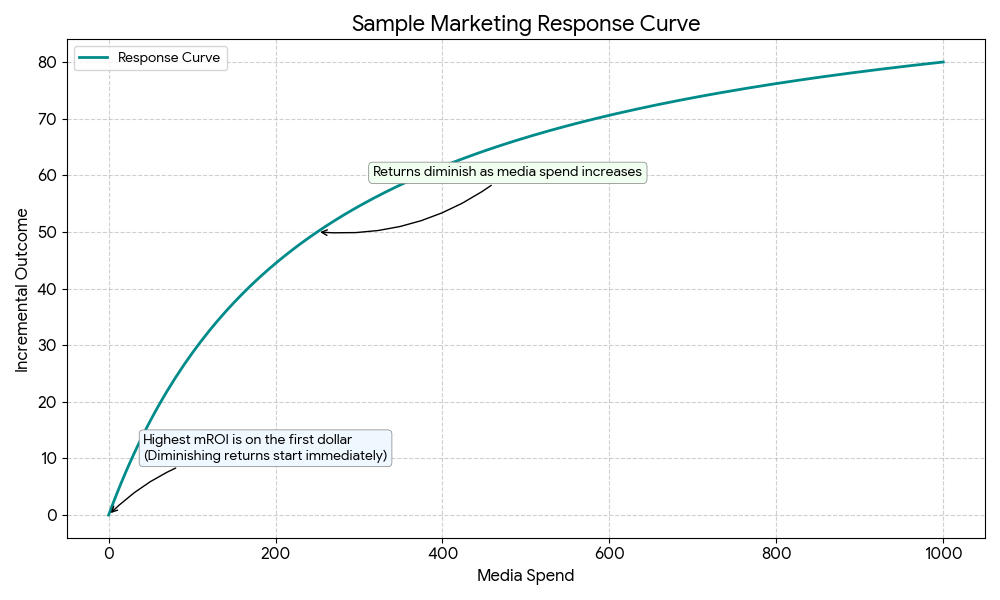
- 响应曲线显示了不同支出水平下的销售额变化情况。它会显示随着支出的不断增加,增加的回报逐渐减少。
- 边际投资回报率是指支出略微增加(例如增加 1 美元)所带来的回报。如果您的渠道接近饱和,边际投资回报率可能只有 0.80 美元,这表示是时候投资其他渠道了。
经验法则建议
- 使用投资回报率评估历史效果:此指标可以清楚地表明,过去在特定渠道上的支出带来了多大的总体效果。
- 使用响应曲线优化未来预算:响应曲线可直观呈现回报递减点,帮助您了解在某个渠道中投资多少金额后,投资回报率会开始下降。
- 使用边际投资回报率评估饱和度:如果边际投资回报率远低于投资回报率,则表明该渠道在当前支出水平下已开始趋于饱和。边际投资回报率最高的渠道最适合投入更多资金。
对照表
| 指标 | 最适合的用途 | 定义 |
|---|---|---|
| 投资回报率 | 评估过往效果。 | 渠道级的历史平均回报率。 |
| 响应曲线 | 优化未来支出和直观呈现回报递减情况。 | 增量效果随支出变化的情况。 |
| 边际投资回报率 | 了解当前饱和度。 | 每新增 1 美元支出所带来的回报。 |
代码示例
如需查看可正常运行的代码示例,请参阅示例 - Meridian 中的投资回报率、边际投资回报率和响应曲线。
详细说明
本部分将深入探讨投资回报率、边际投资回报率和响应曲线的定义和计算方法。
增量效果说明
投资回报率、边际投资回报率和响应曲线的基础是增量效果。增量效果是指由特定营销活动带来的那部分效果(例如销售额或转化次数)。Meridian 通过将实际效果与假设营销活动从未发生的反事实情景进行比较来计算此指标。对于付费媒体,可以通过以下方式进一步了解增量效果与支出的关系:
- 响应曲线可估计任何给定支出水平下的增量效果。
- 投资回报率是指在历史支出水平下获得的增量效果除以支出。
- 边际投资回报率是指在历史预算水平之上额外支出一美元所带来的增量效果。
响应曲线的生成方式
响应曲线可直观呈现单个渠道的支出与增量效果之间的关系,它会假设所有其他渠道的支出都保持不变。
Meridian 会针对渠道的不同支出水平生成此曲线。它会按一定系数(例如历史支出的 1.2 倍)调高或调低渠道的历史支出,估算出每个支出水平下的增量效果。在调整过程中,支出在不同时间和地域的历史分布情况(即排期模式)保持不变。此过程可揭示渠道达到饱和状态的临界点,也就是达到哪个点后进一步投资带来的回报会递减。
解读投资回报率和响应曲线时的注意事项
- 滞后效应:投资回报率的定义使用特定时间段内渠道的总费用作为分母。分子是同一时间段内获得的增量效果。此分子包括在该时间段之前所投广告带来的滞后效应,但不包括在该时间段内所投广告的未来效应。在较长的时间范围(例如一年)内,这对投资回报率估计值的影响较小。不过,对于较短的时间段,影响可能较大。
- 外推风险:为了计算增量效果,模型需要估计支出为零时会发生什么情况。如果您在某个渠道上的支出始终一致,那么模型几乎没有数据来估算这种零支出的情况,因此必须根据其学到的假设进行外推。外推风险还会影响响应曲线上高于历史支出的点的增量效果估计值,并且风险会随着外推程度的增加而增加。
数学附录
本部分介绍了 Meridian 如何定义主要的被估量,包括增量效果、投资回报率、边际投资回报率和响应曲线。这些量使用潜在结果和反事实(因果推理领域的用语)进行定义。
有了明确的被估量定义,您就可以查看营销组合建模分析 (MMM) 提供有效推理所需的假设。这些假设有助于确保模型确实能够估计出这些量。如果不满足假设条件,估计结果可能会出现严重偏差。
我们建议您针对任何 MMM 方法明确定义因果被估量和必要假设。否则,模型结果很可能被误解。影响更大的是,如果忽略了必要假设,分析结果可能会因严重的潜在偏差而变得毫无意义。
下一部分中的定义并不依赖于 Meridian 模型规范的任何方面。同样的定义适用于任何 MMM。定义因果被估量对于任何 MMM 分析都至关重要,这样才能使结果具有可解释性,并有助于确定特定模型在何种假设下才适合进行分析。
增量效果
我们先从增量效果开始,因为它是投资回报率、边际投资回报率和响应曲线的基础。
增量效果背后的因果推理框架
Meridian 会衡量处理变量对效果的因果效应。效果通常是收入,但如果 KPI 不是收入且没有 revenue_per_kpi 数据,Meridian 会将效果定义为 KPI 本身。
我们使用因果推理框架来定义增量效果。在因果推理中,通常使用 \(Y^{(1)}\) 和\(Y^{(0)}\) 这样的符号表示实验反事实情景和对照反事实情景下的潜在结果。Meridian 的模型与之类似,但略微复杂一些,因为其实验反事实情景和对照反事实情景是跨地理位置 $g$、时间 $t$ 和处理变量 $i$ 的三维数组。我们将实验和对照反事实情景分别表示为\(\left\{x^{(1)}_{g,t,i}\right\}\) 和 \(\left\{x^{(0)}_{g,t,i}\right\}\)。此外,潜在结果是一个跨地理位置和时间的二维数组。我们将实验和对照反事实情景下的潜在结果分别表示为\(\overset\sim Y_{g,t}^{\left(\left\{ x_{g,t,i}^{(1)} \right\}\right)}\)和 \(\overset\sim Y_{g,t}^{\left(\left\{ x_{g,t,i}^{(0)} \right\}\right)}\)。
以下表达式有助于在反事实情景之间做出选择:
不过,该数量不可观测,因为无法同时观测两种反事实情景下的潜在结果。实际上最多只能观测一个反事实情景!相反,对于任何两种反事实实验情景(例如 \(\{x^{(1)}_{g,t,i} \}\) 和\(\{ x^{(0)}_{g,t,i} \}\)),应将增量效果定义为:
其中, \(\{z_{g,t,i}\}\) 表示一组控制变量的观测值。使用这个速记符号是为了说明,预期值是以控制随机变量取这些值为条件的。使用 MMM 回归模型和一组精心挑选的控制变量,可以对这一有条件的预期值进行估计。如需了解详情,请参阅使用回归估计增量效果。
通常情况下,系统会针对 \(g=1,\dots G\) 和 \(t=1,\dots T\)求和,但您也可以针对这些值的任何子集定义增量效果。
Meridian 中使用的反事实情景
虽然 incremental_outcome 提供足够的灵活性来考虑任何反事实情景,但 Meridian 默认使用一对特定的反事实实验情景。由于投资回报率、边际投资回报率和响应曲线是基于 incremental_outcome 的默认设置构建的,因此这一对特定情景组合非常重要。
Meridian 将 \(\left\{x^{(1)}_{g,t,i}\right\}\) 设为实际历史值, \(\left\{x^{(0)}_{g,t,i}\right\}\) 与实际历史值相同,但将某个特定处理变量的所有值都设置为其基准值。对于付费媒体和自然媒体,基准值为零。对于非媒体处理变量,基准值可设置为观测到的变量最小值(默认)、最大值或用户提供的浮点值。
对于给定的处理变量 \(q\),增量效果定义为:
\[\text{IncrementalOutcome}_q = \text{IncrementalOutcome} \left(\Bigl\{ x_{g,t,i} \Bigr\}, \Bigl\{ x_{g,t,i}^{(0,q)} \Bigr\} \right)\]
其中:
- \(\left\{ x_{g,t,i}\right\}\) 是观测到的处理变量值
- \(\left\{ x_{g,t,i}^{(0,q)} \right\}\) 表示所有处理变量的观测到的处理变量值,但处理变量 \(q\)除外(该处理变量在所有位置均设置为基准值 \(b_q\) )。更具体地说:
- \(x_{g,t,q}^{(0,q)}=b_q\ \forall\ g,t\)
- \(x_{g,t,i}^{(0,q)}=x_{g,t,i}\ \forall\ g,t,i \neq q\)
需要注意的是,反事实媒体情景 (\(\left\{ x_{g,t,i}^{(0,q)} \right\}\)) 可能实际上并没有在数据中体现出来。在这种情况下,有必要根据模型假设进行外推,以推理出反事实情景。
投资回报率
付费媒体渠道 \(q\) 的投资回报率定义为:
\[\text{ROI}_q = \dfrac{\text{IncrementalOutcome}_q}{\text{Cost}_q}\]
其中, \(\text{Cost}_q\) 是付费媒体渠道 \(q\) 在所有地理位置和时间段的总费用。
请注意,投资回报率的定义使用特定时间段内渠道的总费用作为分母。分子是同一时间段内获得的增量效果。此分子包括在该时间段之前所投广告带来的滞后效应,但不包括在该时间段内所投广告的未来效应。在较长的时间范围(例如一年)内,这对投资回报率估计值的影响较小。不过,对于较短的时间段,影响可能较大。
响应曲线
根据增量效果的定义,付费媒体渠道 \(q\) 的响应曲线被定义为一个函数,该函数以渠道 \(q\)支出函数的形式返回增量效果:
\[\text{IncrementalOutcome}_q (\omega \cdot \text{Cost}_q) = \text{IncrementalOutcome} \left(\left\{ x^{(\omega,q)}_{g,t,i} \right\}, \left\{ x^{(0,q)}_{g,t,i} \right\}\right)\]
其中, \(\left\{ x^{(\omega,q)}_{g,t,i} \right\}\) 表示所有渠道的观测到的媒体值,但渠道 \(q\)除外(该渠道在所有位置的观测到的媒体值均需乘以系数 \(\omega\) )。更具体地说:
- \(x^{(\omega,q)}_{g,t,q}=\omega \cdot x_{g,t,q}\ \forall\ g,t\)
- \(x^{(\omega,q)}_{g,t,i}=x_{g,t,i} \forall\ g,t,i \neq q\)
边际投资回报率 (mROI)
付费媒体渠道 \(q\) 的边际投资回报率 (mROI) 定义为:
其中, \(\delta\) 是一个较小的量,例如 \(0.01\)。
请注意,响应曲线和边际投资回报率的定义隐含了一个假设,即每个媒体单位的费用保持不变,始终等于每个媒体单位的历史平均费用。
