Variables de contrôle

Accéder à :

• Présentation des variables de contrôle
• Sélectionner des variables de contrôle
• Extraire des échantillons a posteriori et a priori des coefficients de contrôle
• Inclure le volume de requêtes comme variable de contrôle
• Utiliser des variables différées
• Variables de contrôle de la mise à l'échelle de la population
• Raisons pour lesquelles les contrôles n'ont pas d'inférence causale ni de répartition de référence

Présentation des variables de contrôle

Les contrôles sont des variables du modèle qui ne sont pas des variables de traitement. Les variables de contrôle sont utilisées pour estimer le résultat de référence, qui correspond au résultat attendu dans le scénario contrefactuel où chaque variable de traitement est définie sur sa valeur de référence pour toutes les zones géographiques et périodes. La valeur de référence est toujours égale à zéro pour les variables média, mais elle est souvent différente de zéro pour les traitements non média. Les variables de contrôle permettent de mieux estimer le résultat de référence et l'effet causal des variables de traitement sur le résultat.

Elles peuvent être classées comme suit :

• Variables de confusion : elles ont un effet causal à la fois sur les traitements et le KPI. Leur inclusion permet de réduire le biais des estimations causales des traitements sur le KPI.

• Variables de prédiction : elles ont un effet causal sur le KPI, mais rien d'autre. Leur inclusion ne réduit pas les biais de l'effet causal des traitements. Toutefois, des prédicteurs forts peuvent réduire la variance des estimations causales.

Les variables de médiation constituent un autre type de variable. Il s'agit de variables qui se trouvent dans le chemin causal entre le traitement et le KPI. En d'autres termes, elles ont un effet causal sur le KPI et sont affectées de manière causale par les traitements. Les variables de médiation ne doivent pas être incluses en tant que variables de contrôle, car cela biaiserait les estimations de l'inférence causale sur les variables de traitement.

Les relations causales entre les types de variables sont expliquées dans le graphe orienté acyclique (DAG, directed acyclic graph) causal suivant, dans le but d'obtenir l'effet causal des médias sur le KPI. Dans les noms de nœuds, le chiffre 1 indique les valeurs de variables à la période 1, le chiffre 2 les valeurs de variables à la période 2 et ainsi de suite. La figure n'affiche que les nœuds pour les périodes 1 et 2, mais supposez qu'elle se poursuit pendant \(T\) périodes.

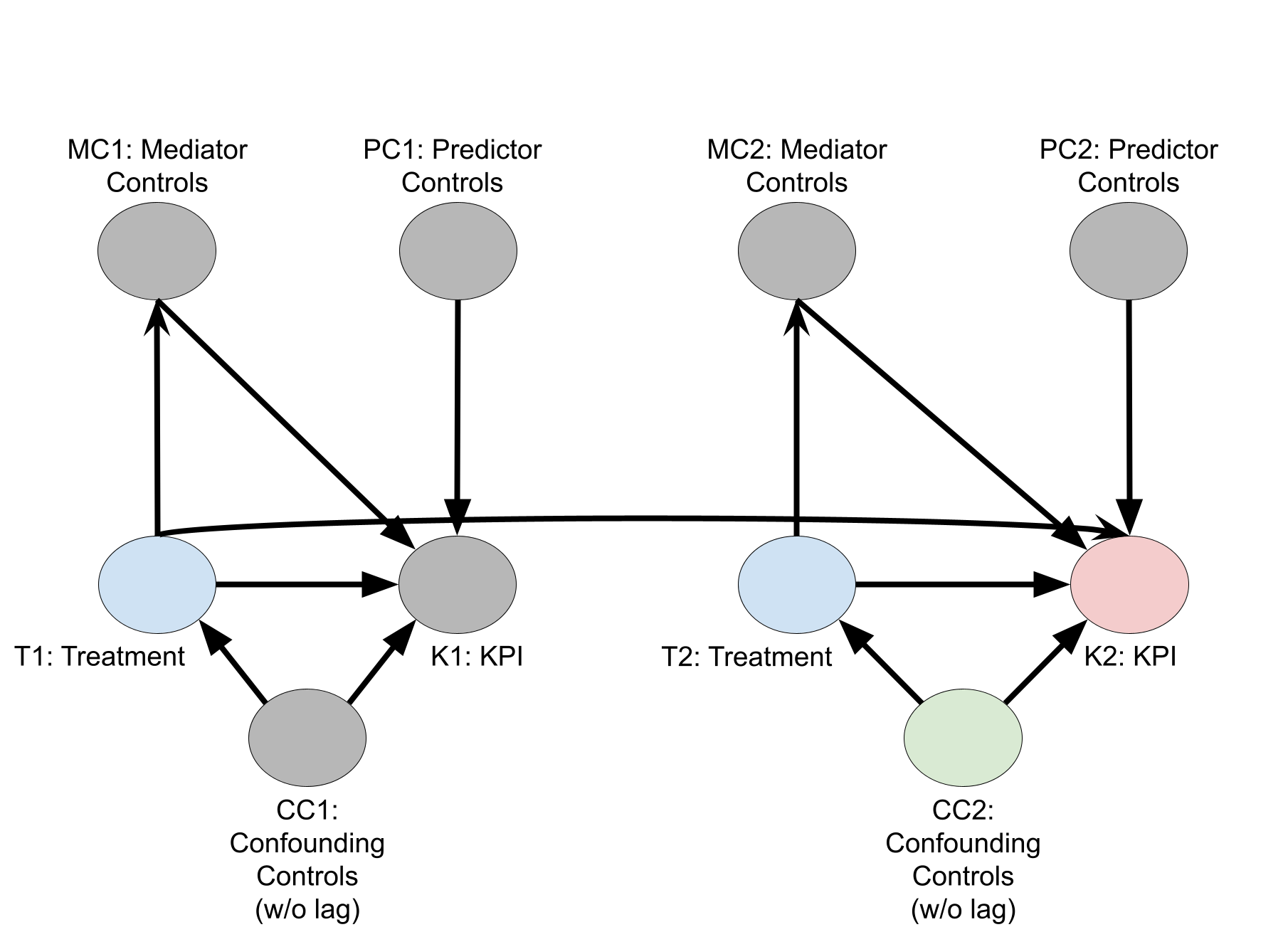
Sélectionner des variables de contrôle

L'objectif de la modélisation du mix marketing (MMM) est d'évaluer l'inférence causale sur les effets média, et non la précision des prédictions. L'objectif principal des variables de contrôle est donc d'améliorer l'inférence sur l'effet causal des traitements appliqués au KPI. Il n'est pas nécessaire ni conseillé d'inclure toutes les variables de prédiction susceptibles d'améliorer la précision des prédictions dans l'échantillon ou en dehors de celui-ci. Des améliorations mineures de la précision des prédictions ne garantissent pas une meilleure précision de l'inférence causale. Si vous utilisez trop de variables de prédiction, la variance des estimations causales pourra augmenter, tout comme le risque de biais d'erreur de spécification du modèle.

Lorsque vous réfléchissez à d'éventuelles variables de confusion à inclure dans le modèle, nous vous conseillons de vous concentrer sur celles qui affectent les décisions marketing ou qui ont un impact sur les décideurs. En effet, la plupart des variables qui affectent les décisions marketing ont également un impact sur les KPI et sont donc des facteurs de confusion. À l'inverse, il est presque impossible de créer une liste complète des variables qui affectent les KPI. Ces variables ne sont pas des facteurs de confusion, sauf si elles influent également sur les décisions marketing.

En principe, les responsables marketing peuvent fournir une liste de toutes les informations quantifiables qui ont été utilisées pour prendre des décisions budgétaires. En réalité, il peut être difficile de compiler une liste complète. Voici quelques questions de base pour les responsables marketing :

1. Au niveau annuel ou trimestriel, comment ont-ils déterminé leur budget média total ?
2. Comment ont-ils décidé de le répartir entre les différents canaux média ?
3. Chaque année, comment ont-ils déterminé les semaines où le budget était élevé et celles où il était faible ?
4. Existe-t-il des pics de dépenses correspondant à certains événements tels que les fêtes ou les lancements de produits ?
5. Pour les questions 1 à 4, quelles sources de données sont les plus corrélées aux décisions budgétaires ? Par exemple, les valeurs de KPI ou les variables économiques des années précédentes ?
6. Ont-ils diffusé des médias naturels, et qu'est-ce qui a motivé cette décision ?
7. Des traitements non média ont-ils été utilisés, et quelle a été la méthode pour décider quand et comment appliquer ces changements ?

En fin de compte, pour vos variables de contrôle, nous vous recommandons :

• d'inclure des variables de confusion ;
• d'exclure les variables de médiation ;
• d'inclure des prédicteurs forts qui peuvent réduire la variance des estimations causales ;
• de ne pas inclure trop de variables dans le seul but d'optimiser la précision prédictive, car cela peut augmenter le risque de biais de spécification incorrecte du modèle.

Extraire des échantillons a posteriori et a priori des coefficients de contrôle

Les échantillons a posteriori et a priori des coefficients de contrôle sont stockés dans l'objet Meridian. Vous pouvez les extraire pour créer des intervalles ou d'autres métriques récapitulatives pouvant vous aider à déterminer quels sont les contrôles adaptés.

Si le nom de l'objet Meridian est mmm, les échantillons a posteriori et a priori des coefficients de contrôle peuvent être trouvés avec mmm.inference_data.prior.gamma_c et mmm.inference_data.posterior.gamma_c, respectivement.

Inclure le volume de requêtes comme variable de contrôle

Comme indiqué dans Sélectionner des variables de contrôle, il est nécessaire d'inclure des variables de confusion pour réduire les biais de l'effet causal des traitements sur le KPI. Vous devez également exclure les variables de médiation pour obtenir des estimations causales non biaisées. Le volume de requêtes peut être un médiateur pour certains canaux média, mais une variable de confusion pour d'autres. Par exemple, le volume de requêtes est certainement une variable de confusion pour les annonces sur le Réseau de Recherche, car une requête pertinente est souvent un prérequis pour ce type d'annonce. Toutefois, d'autres formes de médias peuvent avoir une influence sur le comportement de recherche. Le volume de requêtes est donc une variable de médiation pour ces canaux média. Pour en savoir plus, consultez Modélisation de la recherche sponsorisée.

Étant donné que vous souhaitez estimer l'effet du traitement conjoint de tous les traitements, vous utilisez un seul modèle pour l'inférence. Vous devez donc décider d'inclure le volume de requêtes dans le modèle (en supposant qu'il s'agit d'une variable de confusion) ou de l'exclure de celui-ci (en supposant qu'il s'agit d'une variable de médiation). Tenez compte des points suivants pour choisir votre hypothèse :

• Les canaux pour lesquels il est plus important d'obtenir des estimations non biaisées
• L'étroitesse supposée des liens entre les traitements, le volume de requêtes et le KPI
• Le nombre supposé de canaux où le volume de requêtes est une variable de confusion plutôt qu'une variable de médiation

Nous pensons que la meilleure décision consiste généralement à supposer que le volume de requêtes est une variable de confusion et à l'inclure dans le modèle en raison du lien relativement étroit entre le volume de requêtes et les supports de recherche. Toutefois, la décision dépend du cas d'utilisation.

Utiliser des variables différées

Pour certaines variables de contrôle \(Z\), il peut être judicieux d'inclure des valeurs différées. Par exemple, pour chaque semaine \(t\), incluez \(Z_{t-1},\dots ,Z_{t-L}\)pour une valeur de \(L\). Nous vous recommandons de ne le faire que si vous pensez que les valeurs différées \(t-1, \dots ,t-L\) ont un effet causal sur le KPI pour la semaine \(t\).

Lorsque des contrôles différés ne sont pas nécessaires

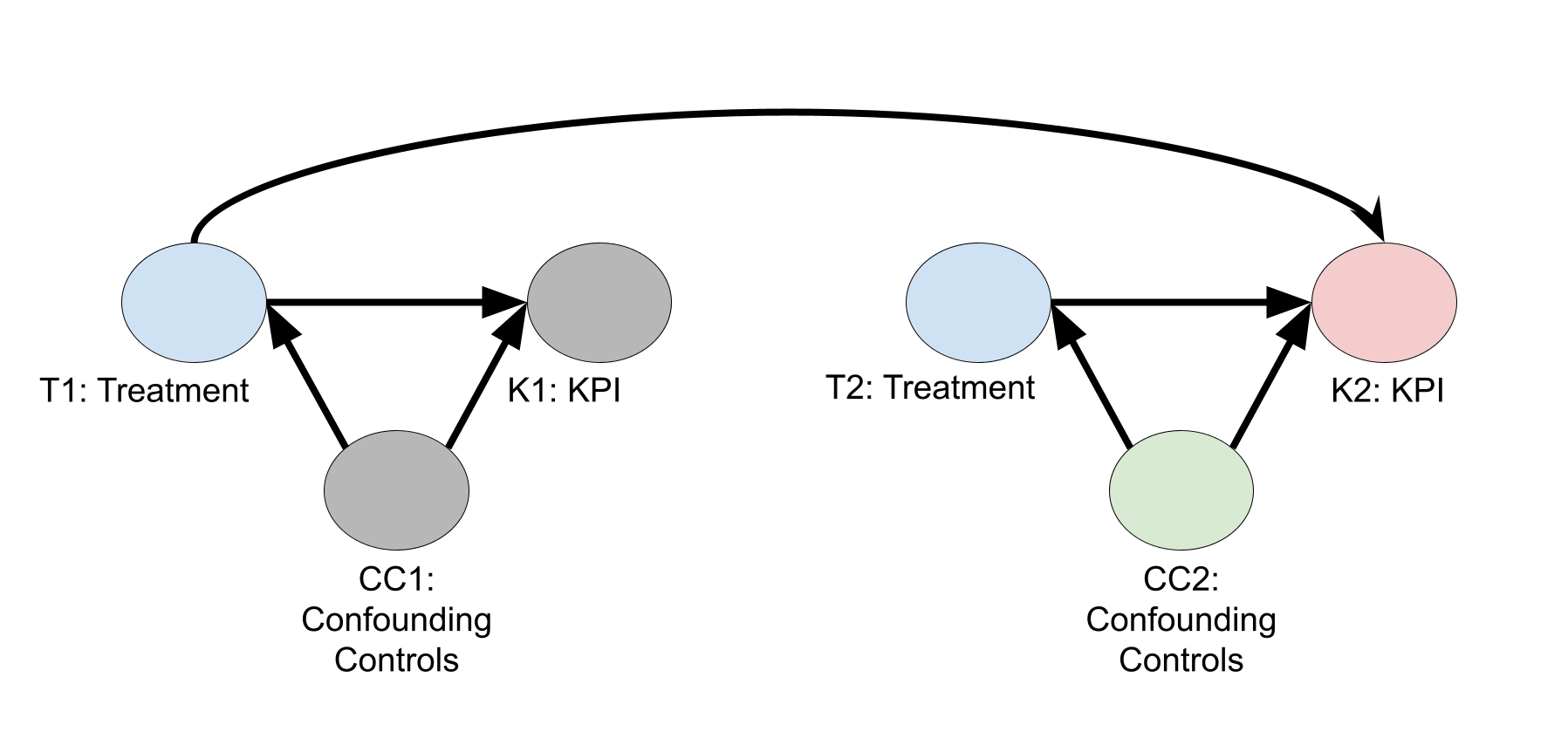
Le diagramme suivant illustre un DAG causal dans lequel les traitements sont supposés avoir un effet différé, mais pas les contrôles. L'hypothèse de ce DAG montre que les contrôles différés ne sont pas nécessaires. Dans les noms de nœuds, le chiffre 1 indique les valeurs de variables à la période 1 et le chiffre 2 les valeurs de variables à la période 2. La figure n'affiche que les nœuds pour les périodes 1 et 2, mais supposez qu'elle se poursuit pendant \(N\) périodes.

À l'aide de critères backdoor (Pearl J., 2009), vous pouvez estimer l'effet causal des traitements sur le KPI de la deuxième semaine en ajustant un modèle de régression pour estimer\(E\bigl( K2 \big| T2,T1,C2 \bigr) = E\bigl( K2^{(T2, T1)} \big| C2 \bigr)\). Les contrôles précédents (\(C1\)) ne sont pas nécessaires.

Lorsque des contrôles différés sont nécessaires

Le diagramme suivant est un DAG causal où des contrôles différés sont nécessaires. Là encore, le nombre dans les noms de nœuds correspond à la période. Pour estimer l'effet causal des traitements sur le KPI de la deuxième semaine, vous devez conditionner les variables de contrôle de la première semaine avec un effet différé sur le KPI. Sinon, un chemin \(T1 \leftarrow L1 \rightarrow K2\)débloqué sera conservé. En utilisant les critères backdoor, vous pouvez ajuster un modèle de régression pour estimer \(E\bigl( K2 \big| T2,T1,C2,L2,L1 \bigr) = E\bigl( K2^{(T2,T1)} \big| C2,L2,L1 \bigr)\).

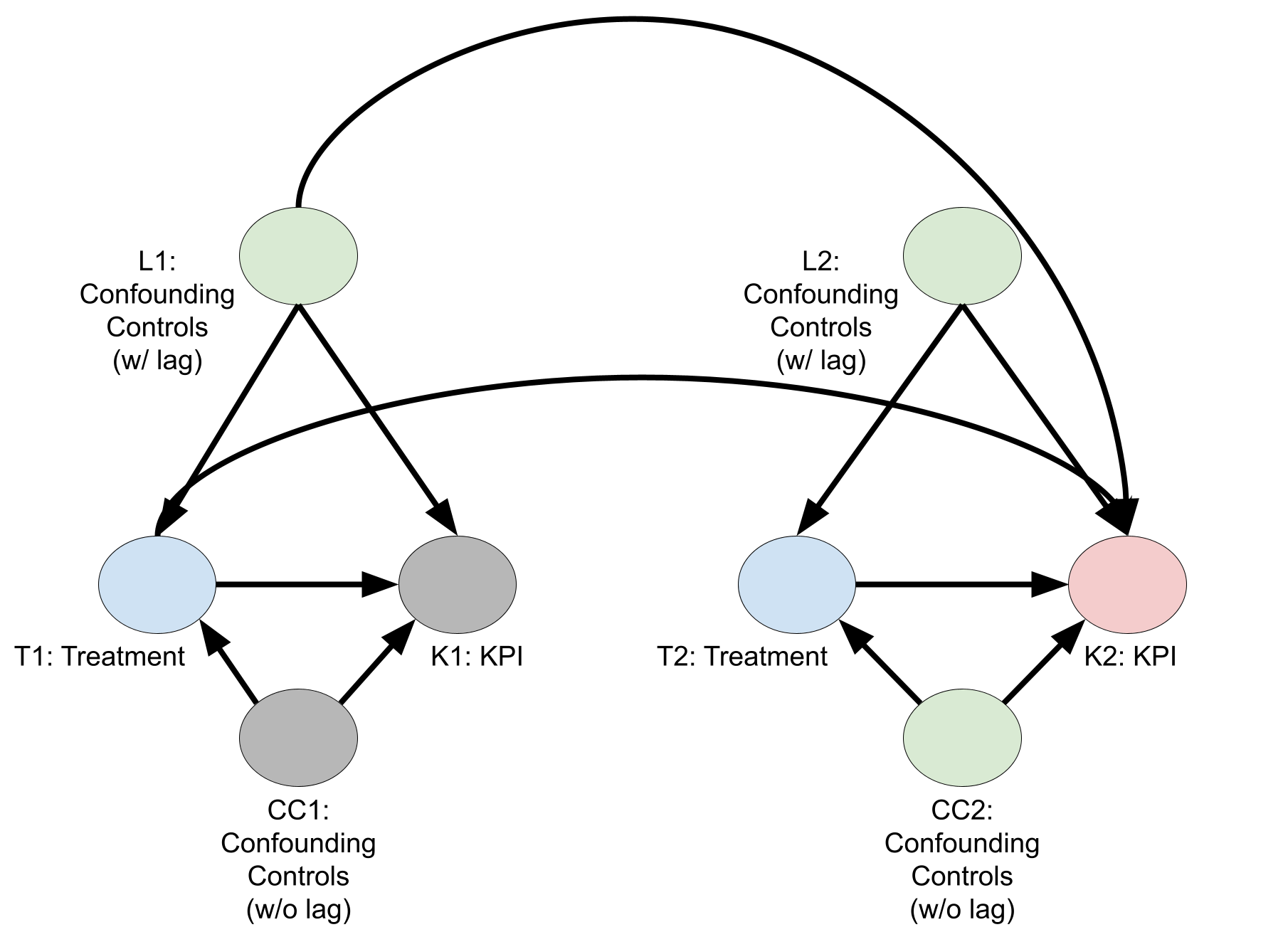
Le diagramme précédent est un DAG simplifié de deux semaines. Toutefois, pour chaque semaine\(t\), vous devez généralement inclure les contrôles de la semaine \(t,t-1, \dots ,t-L\), où\(L\) est le délai le plus long où les contrôles sont encore susceptibles d'affecter le KPI. La valeur de \(L\) peut varier en fonction de la variable de contrôle.

En pratique, vous pouvez tronquer \(L\) à une valeur raisonnable pour éviter de gonfler la variance du modèle en ajoutant trop de variables. Dans de nombreux cas, il peut être raisonnable d'ignorer complètement les contrôles différés si les effets différés sont relativement faibles. Ce type de simplification du modèle peut être considéré comme un compromis entre biais et variance.

Variables de contrôle de la mise à l'échelle de la population

Par défaut, le KPI et l'exécution des médias payants et naturels sont mis à l'échelle selon la population. Les variables de contrôle ne le sont pas par défaut, car certains contrôles, comme la température, ne doivent pas l'être. Toutefois, certaines variables de contrôle, comme les impressions des concurrents, doivent être mises à l'échelle selon la population pour maximiser leur corrélation avec le KPI mis à l'échelle selon la population et avec les variables média. Ces variables peuvent être mises à l'échelle à l'aide de l'argument control_population_scaling_id dans ModelSpec. De même, les traitements non média ne sont pas mis à l'échelle par défaut. Ces variables peuvent être mises à l'échelle à l'aide du non_media_population_scaling_id dans ModelSpec.

Raisons pour lesquelles les contrôles n'ont pas d'inférence causale ni de répartition de référence

Les effets causaux et les pourcentages de contribution sont disponibles pour les traitements média payant, média naturel et non média dans Meridian. Selon le diagramme causal, les effets de régression de ces types de variables peuvent être interprétés comme des effets causaux, contrairement aux effets de régression des variables de contrôle. C'est pourquoi Meridian n'estime pas les effets causaux ni les pourcentages de contribution pour les variables de contrôle.

De plus, Meridian ne décompose pas le résultat de référence en pourcentages d'allocation par variable de contrôle. Certaines variables de contrôle ont naturellement plus d'impact que d'autres sur la précision des prédictions du modèle. Toutefois, c'est plus lié à la variance à laquelle chaque variable contribue dans les estimations du résultat attendu qu'au composant additif de chaque variable dans le calcul du résultat attendu. En réalité, la définition d'une allocation au résultat de référence pour les variables de contrôle serait ambiguë. Une définition possible pourrait être la variation du résultat attendu qui se produit lorsque chaque variable de contrôle est définie sur zéro pour chaque zone géographique et chaque période. Toutefois, cette quantité n'a aucun sens pratique, car elle ne représente ni l'effet causal ni l'importance prédictive de la variable de contrôle. Il est également possible qu'une valeur nulle ne soit pas significative (ni même possible) d'un point de vue pratique pour chaque variable de contrôle, ce qui complique encore plus l'interprétation.

Une variable peut avoir un coefficient et un composant additif importants dans le calcul du résultat attendu, et avoir pourtant peu d'importance en tant que variable de prédiction du KPI. C'est particulièrement vrai pour une variable avec une faible variance. Supprimer une telle variable du modèle peut avoir peu d'impact sur les estimations du résultat attendu si l'effet additif peut être absorbé dans l'interception.

Pour en savoir plus sur ces types de variables, consultez Variables de traitement média naturel et non média.