因果グラフ

前提要件では、バックドア条件を満たす因果グラフを仮定にすると、条件付き交換可能性の仮定が成り立つと述べました。

因果グラフは、変数間の関係を示します。変数はコレクション（ノード）にグループ化され、ノード間の矢印は、その矢印の方向に因果関係が存在する可能性があることを意味します。矢印によって、すべての変数ペアの間に因果関係が存在することが示されるわけではありませんが、どの変数ペアの場合でも、逆方向の因果関係は存在できないことを示しています。

バックドア基準（Pearl, J.、2009 年）では、因果図が与えられた場合に、次の両方が真であれば、変数セット \(Z\) は介入群変数 \(X\) と応答変数 \(Y\) に対するバックドア基準を満たすと述べています。

• \(Z\) 内のノードがいずれも \(X\)の子孫ではなく、かつ
• \(Z\) によって、 \(X\)への矢印を含む \(X\) と \(Y\) 間のすべてのパスがブロックされる

マーケティング ミックス モデリング（MMM）は、有料メディア、オーガニック メディア、メディア以外の変数が KPI（売上など）に及ぼす因果効果を推定するために使用されます。つまり、有料メディア、オーガニック メディア、メディア以外の変数は介入群変数（\(X\)）であり、KPI は応答変数（\(Y\)）です。MMM 回帰からこの因果効果を推定するには、バックドア基準を満たす一連のコントロール変数を慎重に選択して、条件を設定する必要があります。バックドア基準は次のように言い換えることができます。

• メディエーターを制御してはならない。メディエーターは、 \(X\) と \(Y\)の間の因果経路にある変数です。
• すべての交絡因子を制御する必要がある。交絡因子は、 \(X\) と \(Y\)の両方に因果効果を持つ変数です。

MMM のトリートメント変数は、地域と時間の両方でインデックスに登録された有料メディア、オーガニック メディア、メディア以外のトリートメント変数の、任意の組み合わせのコレクションです。トリートメント全体をグラフに表すと扱いにくいため、1 つの地域内の 2 つの期間のみを表す、簡略化したグラフについて考えてみましょう。地域は独立しているという前提になっているため、同じグラフを使用して任意の地域を表すことができます。また、地域間に矢印や関係性はありません。2 つの期間で、遅延トリートメント効果のパターンを十分に説明できます。このパターンは、将来にわたって（または最大遅延時間まで）無制限に繰り返されると想定できます。

下図で、 \(T\) は有料メディア、オーガニック メディア、メディア以外のトリートメント変数、 \(C\) はコントロール、 \(K\) は KPI を表しています。各変数に続く数値は期間を表します。各期間内で、介入群が売上に影響し、コントロールが介入群と売上の両方に影響すると仮定します。次の図では、前の期間の \(T\) が現在の期間の売上に影響しています（「遅延効果」）。メリディアン回帰モデルでは、有料メディアとオーガニック メディアに adstock が適用されますが、メディア以外の介入群には適用されません。これは、実質的には、メディア以外の介入群には遅延効果がないことを前提としています。接続されたノード内の任意の変数ペアの間に因果効果が存在する可能性があることを矢印は示しているため、ノード \(T\) にメディア以外の介入群を含めることは引き続き有効です。ノード \(T\) にメディア以外の介入群を含めると、DAG の表示がクリーンになります。DAG は、バックドア基準を満たす変数を決定するために引き続き有効です。

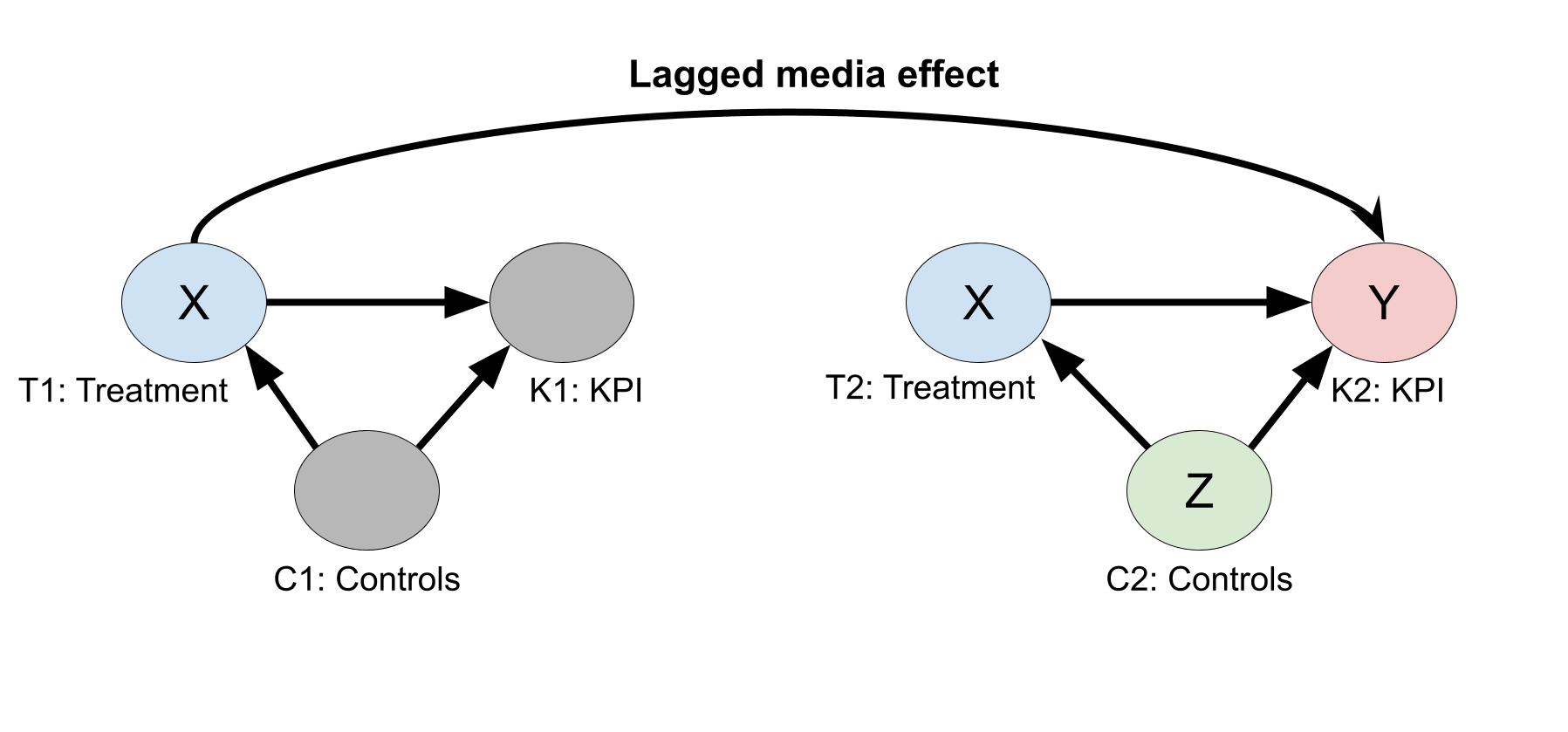
期間 2（\(K2\)）の KPI に対する介入群（\(T1\) と\(T2\)）の因果効果を推定するというタスクを考えてみましょう。グラフから、期間 2 のコントロール（\(C2\)）がバックドア基準を満たしていることがわかります。

軸になる結論は、各期間で、MMM 回帰によって次に対して条件を設定する必要があるということなります。

1. 現在の期間の有料メディアとオーガニック メディア、および想定される最大遅延時間までのすべての前の期間のメディア。
2. 現在の期間のみの、メディア以外のトリートメント変数。
3. 現在の期間のみのコントロール変数。

留意すべき点は次のとおりです。

• \(C1\) から \(C2\) への矢印は、回帰に含める変数には影響しません。
• \(C1\) から \(K2\) への矢印の場合は、回帰に遅延ありのコントロール変数を含める必要があります。実際には、回帰パラメータの数が大幅に増える可能性があるため、可能であればこれは避けた方が賢明です。
• \(T1\) から \(C2\) への矢印の場合は問題があります。この場合、 \(C2\) はメディエーターと交絡因子の両方を兼ねます。1 つの MMM 回帰モデルで、因果的な合同介入群効果を復元することはできません。
• パスの \(T2 \leftarrow K1 \rightarrow K2\) を追加しても、同じ理由で問題になります。その場合、 \(K1\) はメディエーターと交絡因子の両方を兼ねます。