In diesem Abschnitt werden die wichtigsten Messwerte von Meridian behandelt: inkrementelles Ergebnis, Return on Investment (ROI), Grenz-ROI und Reaktionskurven.
Schnelles Wissen
Mithilfe von inkrementellem Ergebnis, Return on Investment (ROI), Grenz-ROI und Reaktionskurven lassen sich die Ergebnisse Ihres Modells in eine umsetzbare Geschäftsstrategie umwandeln. Diese Messwerte können Ihnen helfen, die wichtigsten Marketingfragen zu beantworten: „Wie gut haben meine Channels abgeschnitten?“ und „Wo sollte ich meinen nächsten Dollar ausgeben?“
Mithilfe dieser Messwerte können Sie Ihre effizientesten Channels ermitteln, die aktuelle Sättigung besser nachvollziehen und Ihr Budget optimieren, um die Geschäftsergebnisse zu maximieren. Mit Reaktionskurven lässt sich besonders gut visualisieren, welche Auswirkungen höhere Ausgaben auf das inkrementelle Ergebnis haben. Das ist die Grundlage für die datengestützte Budgetzuweisung.
Marketingbeispiel
Angenommen, Sie betreiben einen Onlineshop für Schuhe. Sie geben \$10.000 für einen Video-Media-Channel aus. Mit Ihrem Meridian-Modell stellen Sie fest, dass der Channel Ihnen zu inkrementellem Umsatz in Höhe von \$25.000 verholfen hat.
- Das inkrementelle Ergebnis ist der Wert, den Sie mit Ihrem Marketing erzielt haben. Angenommen, Ihr Gesamtumsatz betrug \$150.000, aber Meridian schätzt, dass der Umsatz ohne die Kampagne \$125.000 betragen hätte. Das inkrementelle Ergebnis ist die Differenz, also \$25.000.
- Ihr ROI beträgt \$2,50 (\$25.000 Umsatz ÷ \$10.000 Kosten). Das bedeutet, dass Sie für jeden ausgegebenen Dollar \$2,50 verdient haben. Weitere Informationen zur Berechnung finden Sie unter Hinweise zur Interpretation von ROI und Reaktionskurven.
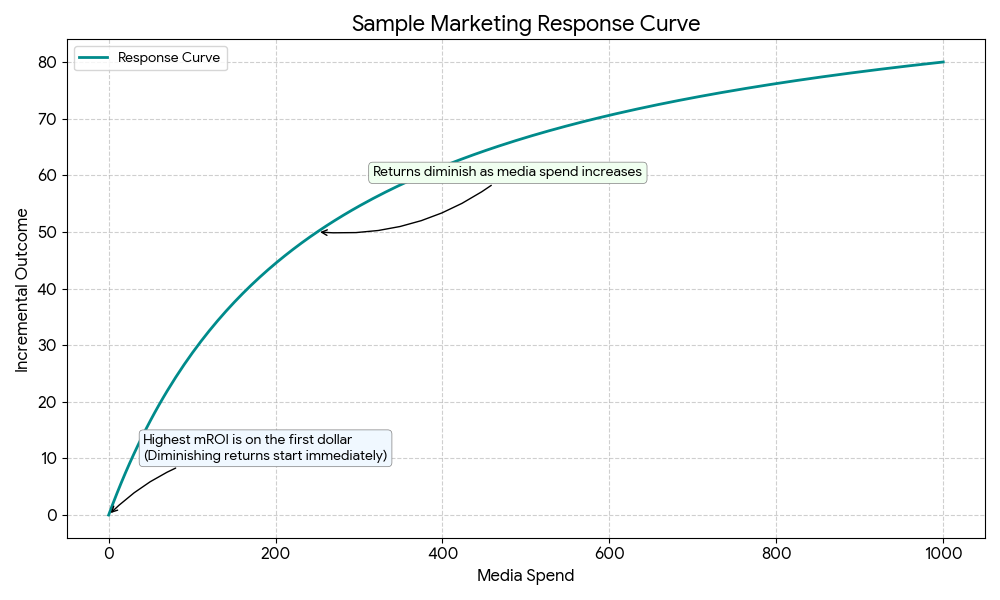
- Die Reaktionskurve zeigt, wie sich Ihr Umsatz bei unterschiedlichen Ausgabenniveaus ändert. Sie verdeutlicht, dass mit steigenden Ausgaben der Umsatz nicht mehr proportional wächst.
- Der Grenz-ROI ist die Rendite, die Sie bei einer geringfügigen Erhöhung der Ausgaben (z. B. dem nächsten Dollar) erzielen würden. Wenn Ihr Channel sich der Sättigungsgrenze nähert, liegt der Grenz-ROI möglicherweise nur noch bei \$0,80, was darauf hindeutet, dass es an der Zeit ist, woanders zu investieren.
Faustregel
- ROI zur Bewertung der bisherigen Leistung verwenden: Er liefert eine klare Gesamtbewertung der Effektivität Ihrer bisherigen Ausgaben für einen bestimmten Channel.
- Reaktionskurven zur Optimierung zukünftiger Budgets verwenden: Sie veranschaulichen den Punkt, ab dem der Grenz-ROI sinkt. So können Sie nachvollziehen, wie viel Sie in einen Channel investieren können, bevor er ineffizient wird.
- Grenz-ROI zur Bewertung des Sättigungsgrads verwenden: Liegt der Grenz-ROI deutlich unter dem ROI, nähert sich der Channel bei den bisherigen Ausgaben der Sättigungsgrenze. Am besten investieren Sie zusätzliche Mittel in die Channels mit dem höchsten Grenz-ROI.
Vergleichstabelle
| Messwert | Optimal für | Definition |
|---|---|---|
| ROI | Bisherige Leistung auswerten | Historischer, channelweiter Durchschnittswert |
| Reaktionskurven | Zukünftige Ausgaben optimieren und abnehmende Renditen visualisieren | Inkrementelles Ergebnis in Abhängigkeit von den Ausgaben |
| Grenz-ROI | Aktuellen Sättigungsgrad nachvollziehen | Rendite für den nächsten ausgegebenen Dollar |
Codebeispiele
Codebeispiele finden Sie hier.
Detaillierte Erklärung
In diesem Abschnitt werden die Definitionen und Methoden für ROI, Grenz-ROI und Reaktionskurven genauer erläutert.
Inkrementelles Ergebnis – Erläuterung
Die Grundlage für ROI, Grenz-ROI und Reaktionskurven ist das inkrementelle Ergebnis. Das ist der Teil Ihres Ergebnisses, z. B. Umsatz oder Conversions, der durch eine bestimmte Marketingaktivität erzielt wurde. Zur Berechnung vergleicht Meridian das tatsächliche Ergebnis mit einem kontrafaktischen Szenario ohne die entsprechende Marketingaktivität. Für bezahlte Medien lässt sich das inkrementelle Ergebnis anhand der Ausgaben weiter in den Kontext setzen:
- Mithilfe der Reaktionskurve lässt sich das inkrementelle Ergebnis für ein beliebiges Ausgabenniveau schätzen.
- Der ROI ist das inkrementelle Ergebnis bei Ihrem bisherigen Ausgabenniveau geteilt durch die Ausgaben.
- Der Grenz-ROI ist das inkrementelle Ergebnis des nächsten ausgegebenen Dollars, der das bisherige Budgetniveau übersteigt.
So werden Reaktionskurven generiert
Eine Reaktionskurve visualisiert das Verhältnis zwischen Ausgaben und inkrementellem Ergebnis für einen einzelnen Channel, wobei davon ausgegangen wird, dass die Ausgaben aller anderen Channels gleich bleiben.
In Meridian wird diese Kurve für verschiedene Ausgabenniveaus für einen Channel generiert. Dabei werden die bisherigen Ausgaben des Channels um einen Faktor (z. B. das 1,2-Fache der bisherigen Ausgaben) nach oben oder unten skaliert und das inkrementelle Ergebnis auf jedem Niveau geschätzt. Die bisherige Verteilung der Ausgaben im Zeitverlauf und nach geografischer Einheit (das Flighting-Muster) wird bei dieser Skalierung beibehalten. So lässt sich ermitteln, ab wann ein Channel gesättigt ist und zusätzliche Investitionen zu einem geringeren ROI führen.
Hinweise zur Interpretation von ROI und Reaktionskurven
- Verzögerte Auswirkungen: Bei der ROI-Definition werden die Gesamtkosten eines Channels über einen bestimmten Zeitraum als Nenner verwendet. Der Zähler ist das inkrementelle Ergebnis, das im selben Zeitraum erzielt wurde. Der Zähler umfasst verzögerte Auswirkungen von Anzeigen, die vor dem Zeitraum ausgeliefert wurden, schließt aber zukünftige Auswirkungen von Anzeigen aus, die während des Zeitraums ausgeliefert wurden. Über einen langen Zeitraum (z. B. ein Jahr) hat dies nur geringe Auswirkungen auf die ROI-Schätzung. Bei kürzeren Zeiträumen kann der Effekt jedoch deutlicher sein.
- Extrapolationsrisiko: Für die Berechnung des inkrementellen Ergebnisses muss das Modell schätzen, was passiert wäre, wenn die Ausgaben null gewesen wären. Wenn Sie immer gleich viel für einen Channel ausgegeben haben, hat das Modell nur wenige Daten für das Szenario ohne Ausgaben und muss auf Grundlage der gelernten Annahmen extrapolieren. Das Extrapolationsrisiko wirkt sich auch auf die Schätzung des inkrementellen Ergebnisses für Punkte auf der Reaktionskurve aus, die über den bisherigen Ausgaben liegen. Das Risiko steigt, je weiter darüber hinausgegangen wird.
Mathematischer Anhang
Hier wird beschrieben, wie Meridian die wichtigsten Schätzgrößen definiert, darunter inkrementelles Ergebnis, ROI, Grenz-ROI und Reaktionskurven. Diese Größen werden anhand potenzieller Ergebnisse und kontrafaktischer Größen definiert, also den Begriffen der kausalen Inferenz.
Wenn die Schätzgrößen eindeutig definiert sind, können Sie die Annahmen prüfen, die für eine gültige Inferenz mit dem MMM erforderlich sind. Diese Annahmen tragen dazu bei, dass das Modell diese Werte auch wirklich schätzen kann. Werden die Annahmen nicht erfüllt, können die Schätzungen stark verzerrt sein.
Wir empfehlen, dass Sie die kausalen Schätzgrößen und die erforderlichen Annahmen für jede MMM-Methodik klar definieren. Andernfalls werden die Modellergebnisse wahrscheinlich falsch interpretiert. Noch schwerwiegender ist, dass die Analyse aufgrund des zugrunde liegenden starken Bias praktisch keinen Sinn mehr ergibt, wenn die erforderlichen Annahmen ignoriert werden.
Die Definitionen im folgenden Abschnitt beruhen nicht auf Aspekten der Meridian-Modellspezifikation. Diese Definitionen können auf alle MMMs angewendet werden. Die Definition der kausalen Schätzgröße ist für jede MMM-Analyse von entscheidender Bedeutung, damit die Ergebnisse interpretierbar sind und um festzustellen, ob ein bestimmtes Modell für die Analyse geeignet ist und unter welchen Annahmen.
Inkrementelles Ergebnis
Wir beginnen mit dem inkrementellen Ergebnis, da es die Grundlage für ROI, Grenz-ROI und Reaktionskurven bildet.
Kausales Inferenzmodell für inkrementelles Ergebnis
In Meridian wird der kausale Effekt von Testvariablen auf das Ergebnis gemessen.
In der Regel ist das der Umsatz. Wenn der KPI jedoch nicht der Umsatz ist und keine revenue_per_kpi-Daten verfügbar sind, definiert Meridian das Ergebnis als den KPI selbst.
Wir definieren das inkrementelle Ergebnis anhand des Frameworks der kausalen Inferenz. In der kausalen Inferenz werden häufig Notationen wie \(Y^{(1)}\) und\(Y^{(0)}\) verwendet, die potenzielle Ergebnisse in kontrafaktischen Test- und Kontrollszenarien darstellen. Meridian ist ähnlich, aber etwas komplexer, da die kontrafaktischen Test- und Kontrollszenarien dreidimensionale Arrays für geografische Einheiten $g$, Zeit $t$ und Testvariablen $i$ sind. Wir bezeichnen die kontrafaktischen Test- und Kontrollszenarien als\(\left\{x^{(1)}_{g,t,i}\right\}\) bzw. \(\left\{x^{(0)}_{g,t,i}\right\}\). Zusätzlich sind die potenziellen Ergebnisse ein zweidimensionales Array für geografische Einheiten und Zeit. Die potenziellen Ergebnisse in den kontrafaktischen Test- und Kontrollszenarien werden als\(\overset\sim Y_{g,t}^{\left(\left\{ x_{g,t,i}^{(1)} \right\}\right)}\)bzw. \(\overset\sim Y_{g,t}^{\left(\left\{ x_{g,t,i}^{(0)} \right\}\right)}\)bezeichnet.
Folgendes ist wichtig, um zwischen kontrafaktischen Szenarien zu entscheiden:
Diese Menge ist jedoch nicht beobachtbar, da sich das potenzielle Ergebnis nicht gleichzeitig in beiden kontrafaktischen Szenarien beobachten lässt. Es kann höchstens ein kontrafaktisches Szenario beobachtet werden. Stattdessen muss für zwei kontrafaktische Testszenarien \(\{x^{(1)}_{g,t,i} \}\) und\(\{ x^{(0)}_{g,t,i} \}\)das inkrementelle Ergebnis so definiert werden:
Dabei bezeichnet \(\{z_{g,t,i}\}\) die beobachteten Werte für eine Reihe von Kontrollvariablen. Mit dieser Kurzschreibweise wird angegeben, dass der Erwartungswert davon abhängt, ob die zufälligen Kontrollvariablen diese Werte annehmen. Mit einem MMM-Regressionsmodell und einer sorgfältig ausgewählten Menge an Kontrollvariablen lässt sich diese bedingte Erwartung schätzen. Weitere Informationen finden Sie unter Inkrementelles Ergebnis mithilfe von Regression schätzen.
Normalerweise wird die Summe über \(g=1,\dots G\) und \(t=1,\dots T\)gebildet. Sie können aber auch das inkrementelle Ergebnis für eine beliebige Teilmenge dieser Werte definieren.
In Meridian verwendete kontrafaktische Szenarien
incremental_outcome bietet zwar genügend Flexibilität, um alle kontrafaktischen Szenarien zu berücksichtigen, standardmäßig verwendet Meridian jedoch ein bestimmtes Paar kontrafaktischer Testszenarien. Da ROI, Grenz-ROI und Reaktionskurven auf den Standardeinstellungen von incremental_outcome basieren, ist dieses spezielle Paar wichtig.
In Meridian sind \(\left\{x^{(1)}_{g,t,i}\right\}\) die tatsächlich beobachteten historischen Werte und \(\left\{x^{(0)}_{g,t,i}\right\}\) die gleichen historischen Werte, wobei jedoch alle Werte für eine bestimmte Testvariable auf ihren Baseline-Wert gesetzt werden. Für kostenpflichtige und organische Medien sind die Baseline-Werte null. Bei nicht mediabezogenen Testvariablen kann der Baseline-Wert auf den beobachteten Mindestwert der Variablen (Standard), den Höchstwert oder einen vom Nutzer angegebenen Gleitkommawert festgelegt werden.
Für eine bestimmte Testvariable \(q\)wird das inkrementelle Ergebnis so definiert:
\[\text{IncrementalOutcome}_q = \text{IncrementalOutcome} \left(\Bigl\{ x_{g,t,i} \Bigr\}, \Bigl\{ x_{g,t,i}^{(0,q)} \Bigr\} \right)\]
Dabei gilt:
- \(\left\{ x_{g,t,i}\right\}\) sind die beobachteten Testwerte.
- \(\left\{ x_{g,t,i}^{(0,q)} \right\}\) steht für die beobachteten Werte für alle Testvariablen mit Ausnahme von Testvariable \(q\), die überall auf ihren Baseline-Wert \(b_q\) gesetzt ist. Noch spezifischer:
- \(x_{g,t,q}^{(0,q)}=b_q\ \forall\ g,t\)
- \(x_{g,t,i}^{(0,q)}=x_{g,t,i}\ \forall\ g,t,i \neq q\)
Das kontrafaktische Media-Szenario (\(\left\{ x_{g,t,i}^{(0,q)} \right\}\)) wird möglicherweise nicht in den Daten widergespiegelt. In diesem Fall ist eine Extrapolation auf Grundlage von Modellannahmen erforderlich, um das kontrafaktische Szenario abzuleiten.
ROI
Der ROI eines kostenpflichtigen Media-Channels \(q\) wird so definiert:
\[\text{ROI}_q = \dfrac{\text{IncrementalOutcome}_q}{\text{Cost}_q}\]
Dabei sind \(\text{Cost}_q\) die Kosten für den kostenpflichtigen Media-Channel \(q\) , summiert über alle geografischen Einheiten und Zeiträume.
Bei der ROI-Definition werden die Gesamtkosten eines Channels über einen bestimmten Zeitraum als Nenner verwendet. Der Zähler ist das inkrementelle Ergebnis, das im selben Zeitraum erzielt wurde. Der Zähler umfasst verzögerte Auswirkungen von Anzeigen, die vor dem Zeitraum ausgeliefert wurden, schließt aber zukünftige Auswirkungen von Anzeigen aus, die während des Zeitraums ausgeliefert wurden. Über einen langen Zeitraum (z. B. ein Jahr) hat dies nur geringe Auswirkungen auf die ROI-Schätzung. Bei kürzeren Zeiträumen kann der Effekt jedoch deutlicher sein.
Reaktionskurven
Verallgemeinert man die Definition des inkrementellen Ergebnisses, wird die Reaktionskurve für den kostenpflichtigen Media-Channel \(q\) als eine Funktion definiert, die das inkrementelle Ergebnis in Abhängigkeit von den Ausgaben für Channel \(q\)zurückgibt:
\[\text{IncrementalOutcome}_q (\omega \cdot \text{Cost}_q) = \text{IncrementalOutcome} \left(\left\{ x^{(\omega,q)}_{g,t,i} \right\}, \left\{ x^{(0,q)}_{g,t,i} \right\}\right)\]
Dabei steht \(\left\{ x^{(\omega,q)}_{g,t,i} \right\}\) für die beobachteten Media-Werte für alle Channels mit Ausnahme von Channel \(q\), der überall mit einem Faktor von \(\omega\) multipliziert wird. Noch spezifischer:
- \(x^{(\omega,q)}_{g,t,q}=\omega \cdot x_{g,t,q}\ \forall\ g,t\)
- \(x^{(\omega,q)}_{g,t,i}=x_{g,t,i} \forall\ g,t,i \neq q\)
Grenz-ROI
Der Grenz-ROI des kostenpflichtigen Media-Channels \(q\) wird so definiert:
Dabei ist \(\delta\) eine kleine Menge wie \(0.01\).
Bei den Definitionen für die Reaktionskurve und den Grenz-ROI wird implizit davon ausgegangen, dass die Kosten pro Media-Einheit konstant sind und den bisherigen durchschnittlichen Kosten pro Media-Einheit entsprechen.
