Earth Engine 提供了多种使用 reducer 执行线性回归的方法:
ee.Reducer.linearFit()ee.Reducer.linearRegression()ee.Reducer.robustLinearRegression()ee.Reducer.ridgeRegression()
最简单的线性回归 reducer 是 linearFit(),它会计算包含常数项的一元线性函数的最小二乘估计值。如需采用更灵活的线性建模方法,请使用线性回归 reducer 之一,该 reducer 支持可变数量的独立变量和因变量。linearRegression() 实现了普通最小二乘回归(OLS)。robustLinearRegression() 使用基于回归残差的成本函数,以迭代方式对数据中的离群值进行减权处理(O’Leary, 1990)。ridgeRegression() 使用 L2 正则化进行线性回归。
使用这些方法进行回归分析适合减少 ee.ImageCollection、ee.Image、ee.FeatureCollection 和 ee.List 对象。以下示例展示了每种方法的应用场景。请注意,linearRegression()、robustLinearRegression() 和 ridgeRegression() 都具有相同的输入和输出结构,但 linearFit() 预期使用双频带输入(X 后跟 Y),并且 ridgeRegression() 具有额外的参数(lambda,可选)和输出(pValue)。
ee.ImageCollection
linearFit()
数据应设置为双波段输入图像,其中第一个波段是自变量,第二个波段是因变量。以下示例展示了气候模型预测的未来降水(NEX-DCP30 数据中的 2006 年之后)线性趋势的估算结果。因变量是预测的降水量,自变量是时间,在调用 linearFit() 之前添加:
Code Editor (JavaScript)
// This function adds a time band to the image. var createTimeBand = function(image) { // Scale milliseconds by a large constant to avoid very small slopes // in the linear regression output. return image.addBands(image.metadata('system:time_start').divide(1e18)); }; // Load the input image collection: projected climate data. var collection = ee.ImageCollection('NASA/NEX-DCP30_ENSEMBLE_STATS') .filter(ee.Filter.eq('scenario', 'rcp85')) .filterDate(ee.Date('2006-01-01'), ee.Date('2050-01-01')) // Map the time band function over the collection. .map(createTimeBand); // Reduce the collection with the linear fit reducer. // Independent variable are followed by dependent variables. var linearFit = collection.select(['system:time_start', 'pr_mean']) .reduce(ee.Reducer.linearFit()); // Display the results. Map.setCenter(-100.11, 40.38, 5); Map.addLayer(linearFit, {min: 0, max: [-0.9, 8e-5, 1], bands: ['scale', 'offset', 'scale']}, 'fit');
请注意,输出包含两个频段:“偏移量”(截距)和“比例”(在本上下文中,“比例”是指线条的斜率,请勿与输入到许多 reducer 的比例参数 [即空间比例] 混淆)。结果应如下所示:上涨趋势区域用蓝色表示,下降趋势区域用红色表示,无趋势区域用绿色表示。

图 1. 应用于预测降水量的 linearFit() 的输出。预计降水量增加的区域显示为蓝色,降水量减少的区域显示为红色。
linearRegression()
例如,假设有两个因变量:降水量和最高温度,以及两个自变量:常量和时间。该集合与上一个示例相同,但必须先手动添加常量频段,然后才能进行缩减。输入的前两个波段是“X”(自变量),后两个波段是“Y”(因变量)。在此示例中,请先获取回归系数,然后扁平化数组图片以提取感兴趣的波段:
Code Editor (JavaScript)
// This function adds a time band to the image. var createTimeBand = function(image) { // Scale milliseconds by a large constant. return image.addBands(image.metadata('system:time_start').divide(1e18)); }; // This function adds a constant band to the image. var createConstantBand = function(image) { return ee.Image(1).addBands(image); }; // Load the input image collection: projected climate data. var collection = ee.ImageCollection('NASA/NEX-DCP30_ENSEMBLE_STATS') .filterDate(ee.Date('2006-01-01'), ee.Date('2099-01-01')) .filter(ee.Filter.eq('scenario', 'rcp85')) // Map the functions over the collection, to get constant and time bands. .map(createTimeBand) .map(createConstantBand) // Select the predictors and the responses. .select(['constant', 'system:time_start', 'pr_mean', 'tasmax_mean']); // Compute ordinary least squares regression coefficients. var linearRegression = collection.reduce( ee.Reducer.linearRegression({ numX: 2, numY: 2 })); // Compute robust linear regression coefficients. var robustLinearRegression = collection.reduce( ee.Reducer.robustLinearRegression({ numX: 2, numY: 2 })); // The results are array images that must be flattened for display. // These lists label the information along each axis of the arrays. var bandNames = [['constant', 'time'], // 0-axis variation. ['precip', 'temp']]; // 1-axis variation. // Flatten the array images to get multi-band images according to the labels. var lrImage = linearRegression.select(['coefficients']).arrayFlatten(bandNames); var rlrImage = robustLinearRegression.select(['coefficients']).arrayFlatten(bandNames); // Display the OLS results. Map.setCenter(-100.11, 40.38, 5); Map.addLayer(lrImage, {min: 0, max: [-0.9, 8e-5, 1], bands: ['time_precip', 'constant_precip', 'time_precip']}, 'OLS'); // Compare the results at a specific point: print('OLS estimates:', lrImage.reduceRegion({ reducer: ee.Reducer.first(), geometry: ee.Geometry.Point([-96.0, 41.0]), scale: 1000 })); print('Robust estimates:', rlrImage.reduceRegion({ reducer: ee.Reducer.first(), geometry: ee.Geometry.Point([-96.0, 41.0]), scale: 1000 }));
检查结果,您会发现 linearRegression() 输出等同于 linearFit() Reducer 估计的系数,但 linearRegression() 输出还包含其他自变量 tasmax_mean 的系数。稳健线性回归系数不同于 OLS 估计值。该示例比较了不同回归方法在特定时间点的系数。
ee.Image
在 ee.Image 对象的上下文中,回归 reducer 可与 reduceRegion 或 reduceRegions 结合使用,对区域中的像素执行线性回归。以下示例演示了如何计算任意多边形中 Landsat 波段之间的回归系数。
linearFit()
介绍数组数据图表的部分显示了 Landsat 8 SWIR1 和 SWIR2 波段之间的相关性散点图。此处计算了此关系的线性回归系数。系统会返回一个字典,其中包含属性 'offset'(y 截距)和 'scale'(斜率)。
Code Editor (JavaScript)
// Define a rectangle geometry around San Francisco. var sanFrancisco = ee.Geometry.Rectangle([-122.45, 37.74, -122.4, 37.8]); // Import a Landsat 8 TOA image for this region. var img = ee.Image('LANDSAT/LC08/C02/T1_TOA/LC08_044034_20140318'); // Subset the SWIR1 and SWIR2 bands. In the regression reducer, independent // variables come first followed by the dependent variables. In this case, // B5 (SWIR1) is the independent variable and B6 (SWIR2) is the dependent // variable. var imgRegress = img.select(['B5', 'B6']); // Calculate regression coefficients for the set of pixels intersecting the // above defined region using reduceRegion with ee.Reducer.linearFit(). var linearFit = imgRegress.reduceRegion({ reducer: ee.Reducer.linearFit(), geometry: sanFrancisco, scale: 30, }); // Inspect the results. print('OLS estimates:', linearFit); print('y-intercept:', linearFit.get('offset')); print('Slope:', linearFit.get('scale'));
linearRegression()
此处应用了上一部分中 linearFit 的相同分析,只不过这次使用的是 ee.Reducer.linearRegression 函数。请注意,回归图像由三张单独的图像构成:一个常量图像,以及表示同一 Landsat 8 图像的 SWIR1 和 SWIR2 波段的图像。请注意,您可以组合任何一组波段来构建输入图片,以便通过 ee.Reducer.linearRegression 进行区域缩减,这些波段不必属于同一源图片。
Code Editor (JavaScript)
// Define a rectangle geometry around San Francisco. var sanFrancisco = ee.Geometry.Rectangle([-122.45, 37.74, -122.4, 37.8]); // Import a Landsat 8 TOA image for this region. var img = ee.Image('LANDSAT/LC08/C02/T1_TOA/LC08_044034_20140318'); // Create a new image that is the concatenation of three images: a constant, // the SWIR1 band, and the SWIR2 band. var constant = ee.Image(1); var xVar = img.select('B5'); var yVar = img.select('B6'); var imgRegress = ee.Image.cat(constant, xVar, yVar); // Calculate regression coefficients for the set of pixels intersecting the // above defined region using reduceRegion. The numX parameter is set as 2 // because the constant and the SWIR1 bands are independent variables and they // are the first two bands in the stack; numY is set as 1 because there is only // one dependent variable (SWIR2) and it follows as band three in the stack. var linearRegression = imgRegress.reduceRegion({ reducer: ee.Reducer.linearRegression({ numX: 2, numY: 1 }), geometry: sanFrancisco, scale: 30, }); // Convert the coefficients array to a list. var coefList = ee.Array(linearRegression.get('coefficients')).toList(); // Extract the y-intercept and slope. var b0 = ee.List(coefList.get(0)).get(0); // y-intercept var b1 = ee.List(coefList.get(1)).get(0); // slope // Extract the residuals. var residuals = ee.Array(linearRegression.get('residuals')).toList().get(0); // Inspect the results. print('OLS estimates', linearRegression); print('y-intercept:', b0); print('Slope:', b1); print('Residuals:', residuals);
系统会返回一个包含 'coefficients' 和 'residuals' 属性的字典。'coefficients' 属性是一个维度为 (numX, numY) 的数组;每个列包含相应因变量的系数。在本例中,数组有两行一列;第一行第一列是 y 截距,第二行第一列是斜率。'residuals' 属性是每个因变量残差的平方根均值的向量。通过将结果转换为数组,然后切片出所需元素,或将数组转换为列表并按索引位置选择系数,提取系数。
ee.FeatureCollection
假设您想了解 Sentinel-2 和 Landsat 8 SWIR1 反射率之间的线性关系。在此示例中,我们使用格式为点地图项集合的随机像素样本来计算这种关系。系统会生成像素对的散点图以及最小二乘法拟合线(图 2)。
Code Editor (JavaScript)
// Import a Sentinel-2 TOA image. var s2ImgSwir1 = ee.Image('COPERNICUS/S2/20191022T185429_20191022T185427_T10SEH'); // Import a Landsat 8 TOA image from 12 days earlier than the S2 image. var l8ImgSwir1 = ee.Image('LANDSAT/LC08/C02/T1_TOA/LC08_044033_20191010'); // Get the intersection between the two images - the area of interest (aoi). var aoi = s2ImgSwir1.geometry().intersection(l8ImgSwir1.geometry()); // Get a set of 1000 random points from within the aoi. A feature collection // is returned. var sample = ee.FeatureCollection.randomPoints({ region: aoi, points: 1000 }); // Combine the SWIR1 bands from each image into a single image. var swir1Bands = s2ImgSwir1.select('B11') .addBands(l8ImgSwir1.select('B6')) .rename(['s2_swir1', 'l8_swir1']); // Sample the SWIR1 bands using the sample point feature collection. var imgSamp = swir1Bands.sampleRegions({ collection: sample, scale: 30 }) // Add a constant property to each feature to be used as an independent variable. .map(function(feature) { return feature.set('constant', 1); }); // Compute linear regression coefficients. numX is 2 because // there are two independent variables: 'constant' and 's2_swir1'. numY is 1 // because there is a single dependent variable: 'l8_swir1'. Cast the resulting // object to an ee.Dictionary for easy access to the properties. var linearRegression = ee.Dictionary(imgSamp.reduceColumns({ reducer: ee.Reducer.linearRegression({ numX: 2, numY: 1 }), selectors: ['constant', 's2_swir1', 'l8_swir1'] })); // Convert the coefficients array to a list. var coefList = ee.Array(linearRegression.get('coefficients')).toList(); // Extract the y-intercept and slope. var yInt = ee.List(coefList.get(0)).get(0); // y-intercept var slope = ee.List(coefList.get(1)).get(0); // slope // Gather the SWIR1 values from the point sample into a list of lists. var props = ee.List(['s2_swir1', 'l8_swir1']); var regressionVarsList = ee.List(imgSamp.reduceColumns({ reducer: ee.Reducer.toList().repeat(props.size()), selectors: props }).get('list')); // Convert regression x and y variable lists to an array - used later as input // to ui.Chart.array.values for generating a scatter plot. var x = ee.Array(ee.List(regressionVarsList.get(0))); var y1 = ee.Array(ee.List(regressionVarsList.get(1))); // Apply the line function defined by the slope and y-intercept of the // regression to the x variable list to create an array that will represent // the regression line in the scatter plot. var y2 = ee.Array(ee.List(regressionVarsList.get(0)).map(function(x) { var y = ee.Number(x).multiply(slope).add(yInt); return y; })); // Concatenate the y variables (Landsat 8 SWIR1 and predicted y) into an array // for input to ui.Chart.array.values for plotting a scatter plot. var yArr = ee.Array.cat([y1, y2], 1); // Make a scatter plot of the two SWIR1 bands for the point sample and include // the least squares line of best fit through the data. print(ui.Chart.array.values({ array: yArr, axis: 0, xLabels: x}) .setChartType('ScatterChart') .setOptions({ legend: {position: 'none'}, hAxis: {'title': 'Sentinel-2 SWIR1'}, vAxis: {'title': 'Landsat 8 SWIR1'}, series: { 0: { pointSize: 0.2, dataOpacity: 0.5, }, 1: { pointSize: 0, lineWidth: 2, } } }) );
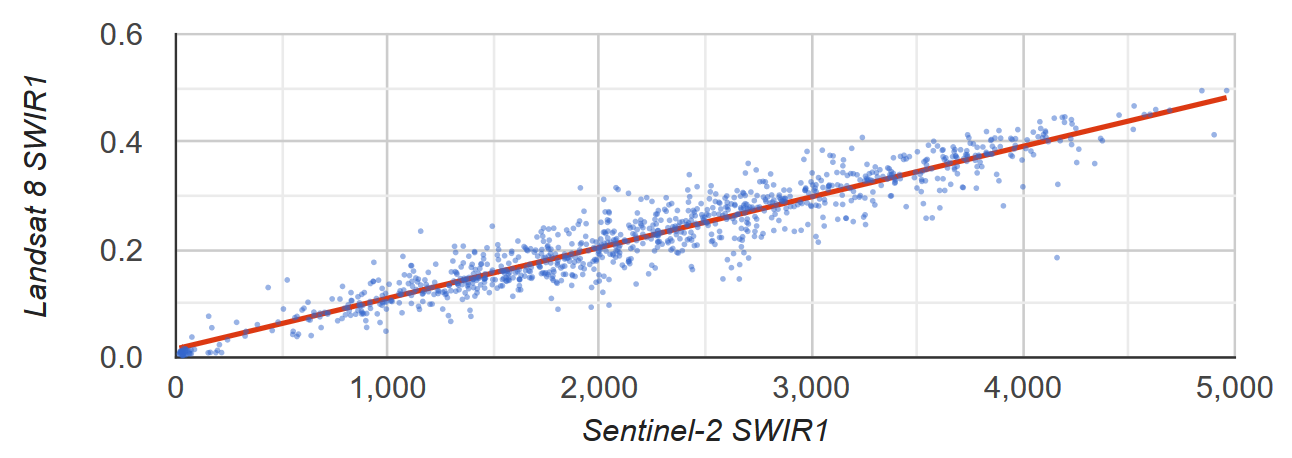
图 2. 代表 Sentinel-2 和 Landsat 8 SWIR1 TOA 反射率的像素样本的散点图和最小二乘法线性回归线。
ee.List
二维 ee.List 对象的列可以作为回归 reducer 的输入。以下示例提供了简单的证明;自变量是因变量的副本,会产生 y 截距等于 0 且斜率等于 1 的直线。
linearFit()
Code Editor (JavaScript)
// Define a list of lists, where columns represent variables. The first column // is the independent variable and the second is the dependent variable. var listsVarColumns = ee.List([ [1, 1], [2, 2], [3, 3], [4, 4], [5, 5] ]); // Compute the least squares estimate of a linear function. Note that an // object is returned; cast it as an ee.Dictionary to make accessing the // coefficients easier. var linearFit = ee.Dictionary(listsVarColumns.reduce(ee.Reducer.linearFit())); // Inspect the result. print(linearFit); print('y-intercept:', linearFit.get('offset')); print('Slope:', linearFit.get('scale'));
如果变量由行表示,请转置列表:转换为 ee.Array、转置,然后转换回 ee.List。
Code Editor (JavaScript)
// If variables in the list are arranged as rows, you'll need to transpose it. // Define a list of lists where rows represent variables. The first row is the // independent variable and the second is the dependent variable. var listsVarRows = ee.List([ [1, 2, 3, 4, 5], [1, 2, 3, 4, 5] ]); // Cast the ee.List as an ee.Array, transpose it, and cast back to ee.List. var listsVarColumns = ee.Array(listsVarRows).transpose().toList(); // Compute the least squares estimate of a linear function. Note that an // object is returned; cast it as an ee.Dictionary to make accessing the // coefficients easier. var linearFit = ee.Dictionary(listsVarColumns.reduce(ee.Reducer.linearFit())); // Inspect the result. print(linearFit); print('y-intercept:', linearFit.get('offset')); print('Slope:', linearFit.get('scale'));
linearRegression()
ee.Reducer.linearRegression() 的应用与上面的 linearFit() 示例类似,但包含一个常量自变量。
Code Editor (JavaScript)
// Define a list of lists where columns represent variables. The first column // represents a constant term, the second an independent variable, and the third // a dependent variable. var listsVarColumns = ee.List([ [1, 1, 1], [1, 2, 2], [1, 3, 3], [1, 4, 4], [1, 5, 5] ]); // Compute ordinary least squares regression coefficients. numX is 2 because // there is one constant term and an additional independent variable. numY is 1 // because there is only a single dependent variable. Cast the resulting // object to an ee.Dictionary for easy access to the properties. var linearRegression = ee.Dictionary( listsVarColumns.reduce(ee.Reducer.linearRegression({ numX: 2, numY: 1 }))); // Convert the coefficients array to a list. var coefList = ee.Array(linearRegression.get('coefficients')).toList(); // Extract the y-intercept and slope. var b0 = ee.List(coefList.get(0)).get(0); // y-intercept var b1 = ee.List(coefList.get(1)).get(0); // slope // Extract the residuals. var residuals = ee.Array(linearRegression.get('residuals')).toList().get(0); // Inspect the results. print('OLS estimates', linearRegression); print('y-intercept:', b0); print('Slope:', b1); print('Residuals:', residuals);
